1º Simulado de Matemática - Petrobras | Transpetro - Banca Cesgranrio
Teste seus conhecimentos com estas 10 questões de matemática baseadas em provas da Cesgranrio para a Petrobras.
Selecione uma alternativa, consulte as dicas se necessário, e depois envie sua resposta para verificar se acertou!
Arthur administra um pequeno negócio de cópias. Atualmente ele possui apenas uma máquina, que é capaz de fazer 50 cópias por minuto, mas pretende comprar mais uma máquina para que possa fazer um total de 7.500 cópias por hora.
Qual a capacidade da máquina que será comprada, em cópias por minuto, para que Arthur alcance o que pretende?
🎓 Dica do Professor:
Transforme todas as unidades para o mesmo padrão (minutos ou horas) antes de calcular. A capacidade total (em cópias por minuto) será a soma da capacidade da máquina já existente com a capacidade da nova máquina.
A questão envolve taxas de trabalho (produtividade).
1. Notação:
Vamos identificar as capacidades das duas máquinas por:
\(M_1\): a capacidade da máquina atual
\(M_2\): a capacidade da nova máquina
2. Capacidade atual:
\(M_1\) = 50 cópias/minuto
3. Meta desejada:
Arthur quer 7.500 cópias por hora. Como 1 hora = 60 minutos, a capacidade total necessária em cópias por minuto é:
\[
\frac{7500}{60} = 125 \, \textbf{cópias/minuto.}
\]
Logo, \(M_1 + M_2 = 125\) cópias por minuto.
4. Capacidade da nova máquina:
Como \(M_1\) = 50, então:
\[
M_2 = 125 - M_1
\]
\[
M_2 = 125 - 50
\]
\[
M_2 = 75
\]
Portanto, a resposta correta é a alternativa E.
Maria comprou 30 balas e 18 chocolates para distribuir entre seus três filhos, mas não os distribuiu igualmente. O filho mais velho recebeu igual número de balas e chocolates, enquanto que o filho do meio ganhou 5 balas a mais do que chocolates. O número de balas que o filho caçula ganhou correspondeu ao dobro do número de chocolates.
Sabendo-se que os dois filhos mais novos de Maria ganharam a mesma quantidade de chocolates, quantas balas couberam ao filho mais velho?
🎓 Dica do Professor:
Ponha nomes (variáveis) para balas e chocolates de cada filho e traduza cada frase do enunciado em equações. Use que os dois mais novos receberam a mesma quantidade de chocolates para reduzir o número de incógnitas. Não esqueça de usar os totais: 30 balas e 18 chocolates.
1. Notação:
Vamos identificar os filhos mais velho, do meio e mais novo de 1, 2 e 3.
As quantidades de balas \(\textbf{(b)}\) e de chocolates \(\textbf{(c)}\) de cada filho por:
- \(b_1, b_2, b_3\) representam as quantidades de balas de cada filho;
- \(c_1, c_2, c_3\) representam as quantidades de chocolates de cada filho;
2. Traduções do enunciado
\(\textbf{2.1}\) Maria comprou 30 balas e 18 chocolates.
\[
b_1 + b_2 + b_3 = 30 \to (1)
\]
\[
c_1 + c_2 + c_3 = 18 \to (2)
\]
\(\textbf{2.2}\) O filho mais velho recebeu igual número de balas e chocolates
\[
b_1 = c_1
\]
\(\textbf{2.3}\) O filho do meio ganhou 5 balas a mais do que chocolates
\[
b_2 = c_2 + 5
\]
\(\textbf{2.4}\) O número de balas que o filho caçula ganhou correspondeu ao dobro do número de chocolates.
\[
b_3 = 2 \cdot c_3
\]
\(\textbf{2.5}\) Os dois filhos mais novos de Maria ganharam a mesma quantidade de chocolates
\[
c_3 = c_2 = x \to (3)
\]
Observe que agora temos que:
\[
b_2 = x + 5 \,\, e \,\, b_3 = 2 \cdot x
\]
3. Vamos reduzir as incógnitas!
Substituindo a relação \(\textbf{(3)}\) na equação \(\textbf{(2)}\), temos:
\[
c_1 + x + x = 18 ⇒ c_1 = 18 \,– 2x \to (4)
\]
4. Vamos usar o total de balas
Sabemos de (1) que:
\[
b_1 + b_2 + b_3 = 30
\]
Já temos os valores de \(b_1, b_2, b_3\) em função de \(x\). Vamos substituílos.
\[
(18 – 2x) + (x + 5) + 2x = 30
\]
\[
23 + x = 30 ⇒ x = 30 \,\,– \,\, 23 ⇒ x = 7
\]
5. Encontrando a quantidade de balas do filho mais velho
Substituindo \(x = 7\) na relação (4).
\[
c_1 = b_1 = 18 \,\, – \,\, 2x ⇒ b_1 = 18 \,\, – \,\, 2 \cdot 7 = 18 \,\, – \,\, 14 = 4
\]
Portanto, o filho mais velho recebeu 4 balas e a resposta correta é a alternativa A.
Em fevereiro, Mário pagou, na conta de seu telefone celular, 264 minutos de ligações. Analisando a conta, ele percebeu que, para cada 3 minutos de ligações para telefones fixos, ele havia feito 8 minutos de ligações para outros telefones celulares. Quantos minutos foram gastos em ligações para telefones celulares?
🎓 Dica do Professor:
Repare que o enunciado fala em uma razão de 3 para 8 entre os minutos de ligações fixo/celular. Isso significa que o total de minutos (264) deve ser dividido em partes proporcionais a 3 e 8.
Basta calcular quanto vale cada parte e depois multiplicar pela quantidade referente às ligações para celular.
1. Notação:
\(\textbf{f =}\) tempo de ligação para telefone fixo
\(\textbf{c =}\) tempo de ligação para celulares
2. A razão dada é 3 : 8.
Isso significa que, a cada 3 minutos de ligações para telefones fixos, temos 8 minutos de ligações para telefones celulares.
\[
\frac{\text{f}}{\text{c}} = \frac{3}{8}
\]
Assim, \(\textbf{f é proporcional a 3}\) e \(\textbf{c é proporcional a 8}\). Traduzindo, temos que:
\[
\textbf{f =} \,\, 3 \cdot k \,\, \to \,\, (1)
\]
\[
\textbf{c =} \,\, 8 \cdot k \,\, \to \,\, (2)
\]
3. O total de minutos gastos foi 264.
Sabemos que:
\[
\textbf{f + c} = 264 \,\, \to \,\, (3)
\]
Substituindo \(\textbf{(1)}\) e \(\textbf{(2)}\) em \(\textbf{(3)}\) temos:
\[
3 \cdot k + 8 \cdot k = 264
\]
\[
11 \cdot k = 264
\]
\[
k = \frac{264}{11} = 24
\]
4. Como as ligações para celular é proporcional a 8 partes, temos:
\[
c = 8 \cdot 24 = 192 min
\]
Portanto, o tempo de ligações para celulares foi de 192 min e a resposta correta é a alternativa E.
A etiqueta com o preço de um computador registra R$ 2.062,50. Esse valor é tal que, mesmo dando um desconto de 20% ao consumidor, ainda há um lucro de 10% sobre o preço de custo.
Qual o preço de custo, em reais, desse computador?
O preço da etiqueta é o preço sem desconto. Ao aplicar 20% de desconto, recebemos 80% do preço de venda.
Esse valor corresponde a 110% do preço de custo, pois há lucro de 10%. Monte a equação considerando essas duas relações.
1. Notação:
Vamos organizzar os diversos tipos de preço do enunciado:
\(P_{final} \,\, \to \,\, \) Preço de venda com desconto
\(P_{custo} \,\, \to \,\, \) Preço que o logista pagou na compra para revenda
2. Preço da etiqueta (preço de venda sem desconto):
\(P_{venda}\) = \(R\$ \,\, 2.062{,}50\)
3. Preço de venda com desconto de 20% sobre o preço de etiqueta:
\(P_{final} = 80\% \,\, \text{de} \,\, P_{venda}\)
\(P_{final} = 80\% \,\, \cdot \,\, R\$ \,\, 2.062{,}50\)
\(P_{final} = 0{,}80 \,\, \cdot \,\, 2.062{,}50\)
\(P_{final} = 1.650{,}00\)
4. Esse valor final é 10% acima do preço de custo (Pc):
\(P_{final} = 110\% \,\, \text{de} \,\, P_{custo}\)
\(1.650{,}00 = 1{,}10\,\, \cdot \,\, P_{custo}\)
\(P_{custo} = \frac{1.650}{1,10} = 1500\)
Portanto, o preço de custo é \(R\$ \,\, 1.500{,}00\) \(\textbf{(alternativa D).}\)
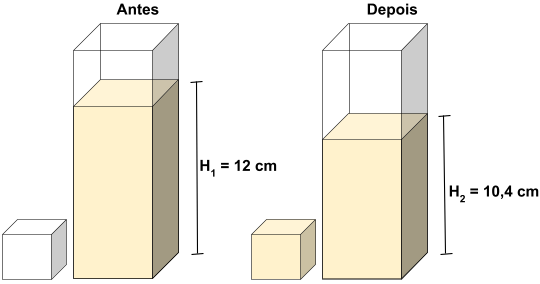
Um recipiente com formato de paralelepípedo reto retângulo, cujas arestas da base medem 5 cm e 8 cm, está parcialmente cheio de água. Despeja-se parte dessa água em um outro recipiente, cúbico e inicialmente vazio, de modo a enchê-lo completamente, como mostra o esquema a seguir.
o volume retirado do paralelepípedo é igual ao volume do cubo.
Em um recipiente de base constante, como é o caso do paralelepípedo, a variação de volume é a área da base multiplicada pela variação de altura do nível da água:
\(V_{transferido} = A_{base} \cdot (H_1 \,\, - \,\, H_2)\)
1. Ilustração.
Na figura abaixo temos uma ilustração do recipiente \(\textbf{(Antes)}\) e de como se deu o processor de transferência de parte do líquido do recipiente para o cubo como você pode ver na figura \(\textbf{(Depois).}\)
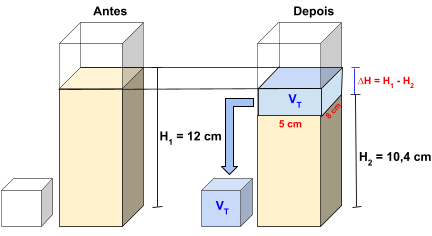
2. Volume transferido (igual ao volume do cubo).
Vamos calcular o volume transferido:
\[
V_T = A_{base} \cdot \Delta H \,\,\, \to \,\,\, \textbf{(1)}
\]
Precisamos dos valores de \(A_{base}\) e \(\Delta H\):
\(A_{base}\) = 5 \(\cdot\) 8 = 40 \(cm^2\).
\(\Delta H = H_{1} - H_{2} = 12,0 – 10,4 = 1,6 \, cm\)
Substituindo os valores encontrados em \(\textbf{(1)}\), temos:
\[
V_T = A_{base} \cdot \Delta H = 40 \cdot 1,6 = 64 \, cm^3
\]
3. Volume do Cubo:
Seja \(a\) a aresta do cubo e sabendo que o volume transferido corresponde ao volume do cubo temos.
\(V_{cubo}\) = \(a^3\)
\(V_T = 64 \, cm^3\)
Logo,
\[
V_{cubo} = V_T
\]
\[
a^3 = 64
\]
\[
a = \sqrt[3]{64}
\]
\[
a = \sqrt[3]{4^3}
\]
\[
a = 4 \, cm
\]
Portanto, a aresta do cubo mede 4 cm \(\textbf{(alternativa B).}\)
Em uma loja, trabalham 8 funcionárias, dentre as quais Diana e Sandra. O gerente da loja precisa escolher duas funcionárias para trabalharem no próximo feriado. Sandra e Diana trabalharam no último feriado e, por isso, não podem ser escolhidas.
Sendo assim, de quantos modos distintos esse gerente poderá fazer a escolha?
🎓 Dica do Professor:
Neste tipo de questão, você pode usar o conceito de combinação, pois a ordem das funcionárias escolhidas não importa.
Primeiramente, observe que Diana e Sandra não podem ser escolhidas. Portanto, o número total de funcionárias disponíveis para escolha é reduzido.
Tente calcular o número de formas de escolher 2 funcionárias entre as restantes.
1. Número total de funcionárias:
A loja tem 8 funcionárias ao todo.
2. Restrições:
Como Diana e Sandra não podem ser escolhidas, restam 6 funcionárias disponíveis para o gerente escolher.
3. Escolha de 2 funcionárias:
O gerente deve escolher 2 funcionárias dentre as 6 disponíveis. Como a ordem não importa, utilizamos a fórmula de combinação:
\[
C_{\text{n,p}} = \frac{n!}{p! \cdot (n- p)!}
\]
Onde:
\(\textbf{n}\) é o número total de opções (6 funcionárias disponíveis),
\(\textbf{p}\) é o número de escolhas (2 funcionárias).
Substituindo na fórmula:
\[
C_{\text{6,2}} = \frac{6!}{2! \cdot (6 - 2)!}
\]
\[
C_{\text{6,2}} = \frac{6!}{2! \cdot 4!}
\]
\[
C_{\text{6,2}} = \frac{6 \cdot 5 \cdot 4!}{2 \cdot 4!} = \frac{6 \cdot 5}{2}
\]
\[
C_{\text{6,2}} = \frac{30}{2} = 15
\]
Portanto, o número de formas distintas de escolher 2 funcionárias entre as 6 disponíveis é 15.
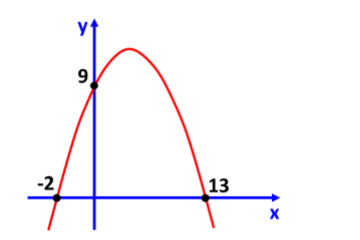
O gráfico de uma função quadrática, mostrado na Figura a seguir, intersecta o eixo y no ponto (0,9), e o eixo x, nos pontos (-2, 0) e (13, 0).
🎓 Dica do Professor:
A equação de uma função quadrática pode ser escrita na forma fatorada em função de suas raízes x₁ e x₂:
f(x) = a • (x - x₁) • (x - x₂)
Neste caso, sabemos que a função intersecta o eixo x nos pontos (-2, 0) e (13, 0), ou seja, as raízes da equação são x₁ = -2 e x₂ = 13.
A partir dessas informações, você pode montar a equação da parábola e, em seguida, substituir x = 11 para encontrar o valor de k.
1. Informações da questão:
- O gráfico intersecta o eixo y no ponto (0, 9), ou seja, f(0) = 9.
- As raízes da função quadrática são \(x_1 = -2\) e \(x_2 = 13\), o que significa que podemos expressar a função quadrática na forma fatorada:
\[
f(x) = a \cdot (x + 2) \cdot (x - 13)\,\, \to \,\, (1)
\]
Onde \(a\) é um coeficiente que ainda precisamos determinar.
2. Determinação do valor de a:
Sabemos que a parábola intercepta o eixo y em (0, 9). Então, substituímos x = 0 e f(0) = 9 na equação (1), temos:
\[
9 = a \cdot (0 + 2) \cdot (0 - 13)
\]
\[
9 = a \cdot 2 \cdot (-13)
\]
\[
9 = -26 \cdot a
\]
\[
a = \frac{-9}{26}
\]
Agora vamos substituir o valor de a na equação (1):
\[
f(x) = \frac{-9}{26} \cdot (x + 2) \cdot (x - 13) \,\,\, \to \,\,\, (2)
\]
3. Encontrando o valor de k para x = 11:
Agora que sabemos que tesmo as equação da parábola, podemos substituir esse valor na equação da função quadrática em (2) podemos determinear o valor de k substituindo quando \(x = 11\) na equação (2).
\[
f(11) = \frac{-9}{26} \cdot (11 + 2) \cdot (11 - 13)
\]
\[
f(11) = \frac{-9}{26} \cdot (13) \cdot (-2)
\]
\[
f(11) = \frac{-9}{26} \cdot (-26)
\]
\[
f(11) = 9
\]
Logo, o valor de k para P(11, k) é 9.
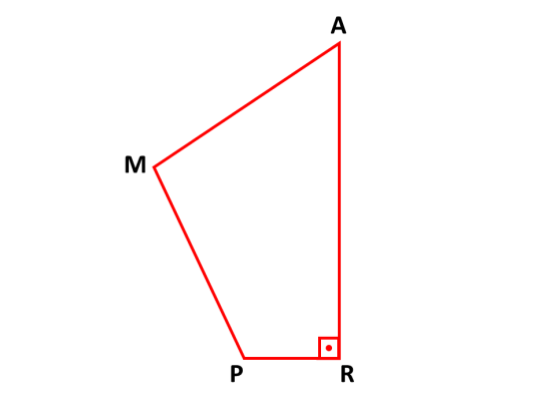
No quadrilátero RAMP, o ângulo R é reto, e os lados PR e RA medem, respectivamente, 6 cm e 16 cm.
Se a área de RAMP é 105 cm², qual é, em cm², a área do triângulo PAM?
🎓 Dica do Professor:
No quadrilátero RAMP, temos um triângulo retângulo RAP com ângulo reto em R, e os lados PR = 6 cm e RA = 16 cm.
A área do quadrilátero RAMP é dada, e o objetivo é determinar a área do triângulo PAM, que faz parte do quadrilátero.
Primeiramente, calcule a área do triângulo RAP, depois use a área total para calcular a área do trapézio AMP e, finalmente, a área do triângulo PAM.
1. Informações fornecidas:
- O quadrilátero RAMP pode ser dividido em duas duas partes triangulares. O triangulo RAP \(\textbf{(figura 1)}\) e o triângulo AMP \(\textbf{(figura 2)}\) conforme figura abaixo.
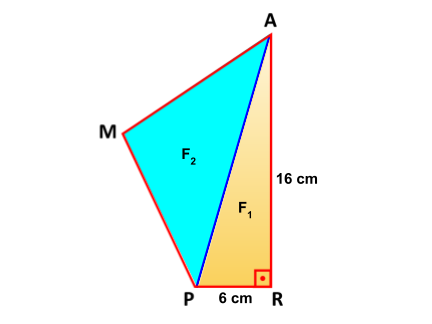
- O triângulo RAP é um triângulo retângulo.
- A área total do quadrilátero RAMP = 105 cm².
2. Calculando a área do triângulo RAP:
O triangulo RAP \(\textbf{(figura 1)}\) é retângulo, então sua área pode ser calculada pela fórmula da área de um triângulo retângulo:
3. Calculando a área do triângulo AMP:
Sabemos que:
\(A_{RAMP} = 105\,\, cm^2\)
\(A_{RAP} = 48 \,\, cm^2\)
Substituindo esse valores em \(\textbf{(1)}\), temos:
\[
105 = 48 + A_{AMP}
\]
\[
A_{AMP} = 105 - 48
\]
\[
A_{AMP} = 57 \,\, cm^2
\]
Logo, a área do triângulo AMP é de 57 cm² e a \(\textbf{alternativa C)}\) é o gabarito da questão.
A magnitude M de um terremoto é expressa, em função da energia liberada "\(x\)", em joules, pela lei \(M(x) = \frac{\left( \log_{10} x \right) - 1{,}44}{1{,}5}\). Um terremoto que libere \(100^3\) joules de energia, terá magnitude M igual a:
🎓 Dica do Professor:
A fórmula que relaciona a magnitude do terremoto M(x) com a energia x é dada por uma expressão logarítmica.
Para resolver a questão, você precisa substituir o valor de \(x = 100^3\) na fórmula fornecida e, em seguida, calcular o valor do logaritmo de \(100^3\).
Lembre-se de que a base do logaritmo é 10 (logaritmo decimal). Após calcular o logaritmo, basta substituir na fórmula para encontrar a magnitude M(x).
1. Fórmula dada:
A fórmula que relaciona a magnitude \(M(x)\) com a energia \(x\) é:
2. Vamos \(x = 100^3\) na fórmula:
Antes perceba que:
\[
100^3 = \left( 10^{2} \right)^3 = 10^6
\]
Então,
\[
M(x) = \frac{\left( \log_{10} 10^6 \right) - 1{,}44}{1{,}5}
\]
Sabemos que: \(\log_{10} \left( 10^6 \right) = 6\)
Agora, substituímos esse valor na fórmula:
\[ M\left( 10^6 \right) = \frac{6 - 1,44}{1,5} \] \[ M\left( 10^6 \right) = \frac{4,56}{1,5} \] \[ M\left( 10^6 \right) = 3,04 \]Portanto, a magnitude M é 3,04 \(\textbf{(alternativa C)}\).
Com o objetivo de identificar a necessidade da criação de uma creche, uma empresa de combustíveis realizou um levantamento entre seus funcionários, por setor e sexo, com o seguinte resultado:
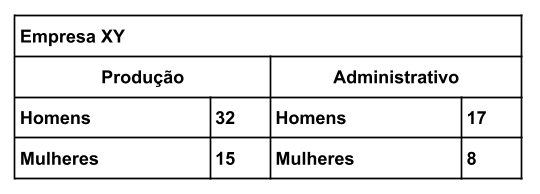
Com base nas informações apresentadas, conclui-se que o número total de homens é superior ao total de mulheres em, aproximadamente,
🎓 Dica do Professor:
Para encontrar a diferença percentual entre o número de homens e o número de mulheres, primeiro calcule o total de homens e o total de mulheres na empresa.
Em seguida, use a fórmula da porcentagem de diferença, comparando o número de homens com o número de mulheres.
A fórmula é: \[ \textbf{Percentual de diferença} = \frac{\textbf{Diferença}}{\textbf{Total de mulheres}} \times 100\% \]
1. Número total de homens:
- Setor de Produção: 32 homens
- Setor Administrativo: 17 homens
\(\textbf{Total de homens = 32 + 17 = 49}\)
2. Número total de mulheres:
- Setor de Produção: 15 mulheres
- Setor Administrativo: 8 mulheres
\(\textbf{Total de mulheres = 15 + 8 = 23}\)
3. Calculando a diferença:
A diferença entre o número de homens e mulheres é:
\(\textbf{49 - 23 = 26 homens a mais do que mulheres}\)
4. Calculando o percentual:
Agora, para calcular o percentual de diferença em relação ao número de mulheres, usamos a fórmula da porcentagem:
Portanto, o número total de homens é superior ao total de mulheres em aproximadamente 113% \(\textbf{(alternativa E)}\).
Vídeo Gabarito:
Quiz de Matemática - Simulado Cesgranrio Petrobras
© 2023 Blog do Professor Micael. Todos os direitos reservados.
