Conteúdos
Questão 1
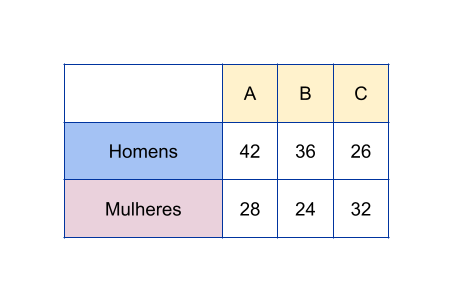
(Espm-2014) A distribuição dos alunos nas 3 turmas de um curso é mostrada na tabela abaixo.
 Escolhendo-se uma aluna desse curso, a probabilidade de ela ser da turma A é:
Escolhendo-se uma aluna desse curso, a probabilidade de ela ser da turma A é:
A questão pede a probabilidade de escolher uma aluna da turma A. Atenção: como estamos escolhendo uma aluna, só devemos considerar o total de mulheres. Faça a soma total de alunas do curso e, em seguida, veja quantas pertencem à turma A. Aplique a fórmula da probabilidade clássica.
Vídeo gabarito:
Questão 2
(Uerj-2019) Um menino vai retirar ao acaso um único cartão de um conjunto de sete cartões. Em cada um deles está escrito apenas um dia da semana, sem repetições: segunda, terça, quarta, quinta, sexta, sábado, domingo. O menino gostaria de retirar sábado ou domingo.
A probabilidade de ocorrência de uma das preferências do menino é:
Comece identificando o total de possibilidades e, em seguida, veja quantas delas são favoráveis ao evento desejado — nesse caso, retirar "sábado" ou "domingo". A questão é direta e envolve apenas contagem simples.
O conjunto de cartões contém sete cartões, um para cada dia da semana:
- segunda
- terça
- quarta
- quinta
- sexta
- sábado
- domingo
\(\textbf{Passo 1:}\) Total de possibilidades
Como há 7 cartões, todos diferentes, o número total de possibilidades é:
\[ \text{total} = 7 \]
\(\textbf{Passo 2:}\) Casos favoráveis
O menino quer sábado ou domingo, ou seja:
\[ \text{n(favoráveis)} = 2 \]
\(\textbf{Passo 3:}\) Cálculo da probabilidade
\[ \text{P(sair sábado ou domingo)} = \frac{2}{7} \]
✅ RESPOSTA CORRETA:
Alternativa D) \(\frac{2}{7}\)
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 3
(Uftm-2012) Em certo jogo de perguntas e respostas, o jogador ganha 3 pontos a cada resposta correta e perde 5 pontos a cada resposta errada. Paulo respondeu 30 perguntas e obteve um total de 50 pontos. Selecionando-se aleatoriamente uma das perguntas feitas a Paulo, a probabilidade de que ela seja uma das que tiveram resposta incorreta é de:
Transforme a situação em uma equação: use uma variável x para representar o número de erros e 30 - x para acertos. Lembre-se de que o total de perguntas foi 30 e o saldo de pontos foi 50. Depois, encontre a quantidade de erros e use-a para calcular a probabilidade.
Passo 1: Definir variáveis
Seja:
- x: número de erros
- 30 - x: número de acertos
Sabemos que:
\[ \text{nº de acertos} + \text{nº de erros} = 30 \]
E que cada acerto vale +3 pontos e cada erro vale –5 pontos, totalizando 50 pontos:
\[ 3 \cdot (30 - x) - 5 \cdot x = 50 \]
Passo 2: Resolver a equação
\[ 3 \cdot (30 - x) - 5 \cdot x = 50 \]
\[ 90 - 3 \cdot x - 5 \cdot x = 50 \]
\[ -8 \cdot x = 50 - 90 \]
\[ -8 \cdot x = -40 \]
Multiplicando os dois membros por (-1), temos
\[ 8 \cdot x = 40 \]
\[ x = \frac{40}{8} = 5 \]
Passo 3: Calcular a probabilidade de uma pergunta errada
\[ P(\text{erro}) = \frac{5}{30} = \frac{1}{6} \]
✅ RESPOSTA CORRETA:
Alternativa D) \(\frac{1}{6}\)
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 4
(IFSP-2016) O gráfico abaixo apresenta informações sobre os números de livros lidos no mês passado pelos alunos de uma determinada turma. Sabendo-se que a informação de todos os alunos consta nesse gráfico, e que não há aluno que leu mais de 3 livros, utilize-o para responder a questão.
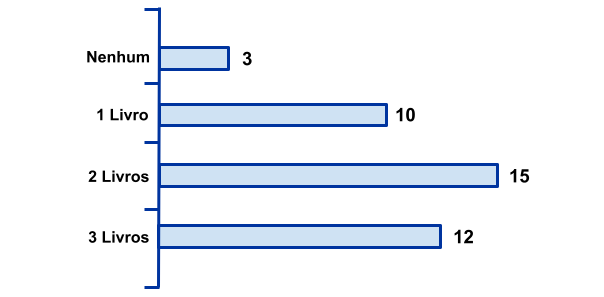
Escolhido aleatoriamente um aluno dessa turma, a probabilidade de o aluno escolhido não ter lido livro no mês passado é:
Some o número total de alunos. Depois, divida o número de alunos que não leram livros pelo total e multiplique por 100 para encontrar a porcentagem.
- Total de alunos:
\[ 3 + 10 + 15 + 12 = 40 \] - Alunos que não leram livros: 3.
- Probabilidade:
\[ \frac{3}{40} = 0,075 = 7,5\% \]
✅ RESPOSTA CORRETA:
Alternativa E) 7,5%
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 5
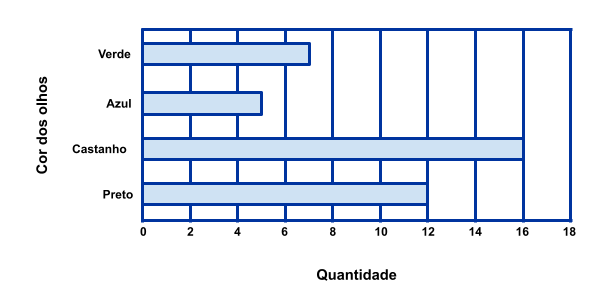
(FACEMA-2009) Os 40 alunos de uma sala de aula têm a cor dos olhos bem definida e a distribuição das quantidades pode ser obtida pelo diagrama de barras da figura. Escolhendo-se, ao acaso, um aluno dessa sala de aula, a probabilidade de que tenha olhos azuis é:
1º) Lembre-se de que a probabilidade é dada pela razão entre o número de casos favoráveis e o número de casos possíveis.
2º) Identifique primeiro quantos alunos têm olhos azuis e quantos alunos há no total.
1º) Total de alunos na sala:
\[ 7 \; (\text{verdes}) + 5 \; (\text{azuis}) + 16 \; (\text{castanhos}) + 12 \; (\text{pretos}) = 40. \]
2º) Casos favoráveis (alunos com olhos azuis):
\[ 5. \]
3º) Probabilidade de escolher um aluno com olhos azuis:
\[ \frac{\text{casos favoráveis}}{\text{total de casos}} = \frac{5}{40} = \frac{1}{8}. \]
4º) Convertendo para porcentagem:
\[ \frac{1}{8} \times 100\% = 12,5\%. \]
✅ RESPOSTA CORRETA:
Alternativa A) 12,5%.
Vídeo gabarito:
Questão 6
(Unesp-2014) Em um condomínio residencial, há 120 casas e 230 terrenos sem edificações. Em um determinado mês, entre as casas, 20% dos proprietários associados a cada casa estão com as taxas de condomínio atrasadas, enquanto que, entre os proprietários associados a cada terreno, esse percentual é de 10%. De posse de todos os boletos individuais de cobrança das taxas em atraso do mês, o administrador do empreendimento escolhe um boleto ao acaso. A probabilidade de que o boleto escolhido seja de um proprietário de terreno sem edificação é de:
Comece identificando o total de boletos em atraso (casas e terrenos). Depois, veja a fração que corresponde aos terrenos. Lembre-se: probabilidade é a razão entre o número de casos favoráveis e o número total de casos possíveis.
- Número de casas com atraso:
\[ 0,20 \times 120 = 24. \] - Número de terrenos com atraso:
\[ 0,10 \times 230 = 23. \] - Total de boletos em atraso:
\[ 24 + 23 = 47. \] - Probabilidade de o boleto ser de terreno:
\[ \frac{23}{47}. \]
✅ RESPOSTA CORRETA:
Alternativa E) \(\frac{23}{47}\)
Vídeo gabarito:
Questão 7
(Enem 2018) O gerente do setor de recursos humanos de uma empresa está organizando uma avaliação em que uma das etapas é um jogo de perguntas e respostas. Para essa etapa, ele classificou as perguntas, pelo nível de dificuldade, em fácil, médio e difícil, e escreveu cada pergunta em cartões para colocação em uma urna.
Contudo, após depositar vinte perguntas de diferentes níveis na urna, ele observou que 25% deles eram de nível fácil. Querendo que as perguntas de nível fácil sejam a maioria, o gerente decidiu acrescentar mais perguntas de nível fácil à urna, de modo que a probabilidade de o primeiro participante retirar, aleatoriamente, uma pergunta de nível fácil seja de 75%.
Com essas informações, a quantidade de perguntas de nível fácil que o gerente deve acrescentar à urna é igual a
Comece descobrindo quantas das 20 perguntas iniciais são de nível fácil. Depois, chame de x a quantidade de novas perguntas fáceis que serão adicionadas. Monte uma equação para garantir que a nova proporção de perguntas fáceis seja 75%. Resolva a equação.
Passo 1: Informações iniciais
O total inicial de perguntas na urna é 20, e 25% são fáceis:
\[ 0,25 \times 20 = 5 \text{ (perguntas fáceis)} \]
Passo 2: Acrescentar x perguntas fáceis
Se o gerente adicionar \(x\) perguntas fáceis:
\[ \text{Total de perguntas: } 20 + x \]
\[ \text{Total de fáceis: } 5 + x \]
Ele quer que a nova proporção de perguntas fáceis seja 75%, ou seja:
\[ \frac{5 + x}{20 + x} = 0,75 \]
Passo 3: Resolver a equação
\[ 5 + x = 0,75(20 + x) \]
\[ 5 + x = 15 + 0,75x \]
\[ x - 0,75x = 15 - 5 \]
\[ 0,25x = 10 \Rightarrow x = \frac{10}{0,25} = 40 \]
✅ RESPOSTA CORRETA:
Alternativa D) 40
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 8
(Ufms-2020) Em uma pequena propriedade rural da cidade de Aquidauana, há três raças de gado de corte: Nelore, Girolando e Pantaneira. O rebanho é composto por 40 cabeças, sendo 25 cabeças da raça Nelore, 10 da raça Girolando e 5 da raça Pantaneira. Para uma exposição agropecuária, serão enviadas 3 cabeças. Escolhendo ao acaso, qual a probabilidade de as três cabeças escolhidas para a exposição serem da raça Girolando?
Use a fórmula da combinação para calcular a quantidade de maneiras de escolher 3 cabeças de gado entre as 40. Depois, aplique novamente a fórmula para descobrir de quantas maneiras é possível escolher 3 cabeças somente da raça Girolando (há 10 disponíveis). Por fim, monte a fração da probabilidade com essas duas quantidades.
Passo 1: Total de cabeças no rebanho
\[ \text{Total de cabeças: } 25 (\text{Nelore}) + 10 (\text{Girolando}) + 5 (\text{Pantaneira}) = 40 \]
Passo 2: Total de formas de escolher 3 cabeças do rebanho
\[ \mathrm{C}_{40,3} = \frac{40 \cdot 39 \cdot 38}{3 \cdot 2 \cdot 1} = 20 \cdot 13 \cdot 38 = 9.880 \]
Passo 3: Casos favoráveis — escolher 3 cabeças da raça Girolando
\[ \mathrm{C}_{10,3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120 \]
Passo 4: Calcular a probabilidade
\[ P(3 \text{ Girolandos}) = \frac{120}{9880} = \frac{3}{247} \]
✅ RESPOSTA CORRETA:
Alternativa C) \(\frac{3}{247}\)
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 9
(Faculdade Albert Einstein-2016) Em uma urna vazia foram colocadas fichas iguais, em cada uma das quais foi escrito apenas um dos anagramas da palavra HOSPITAL. A probabilidade de que, ao sortear-se uma única ficha dessa urna, no anagrama nela marcado as letras inicial e final sejam ambas consoantes é:
Primeiro, conte o total de anagramas possíveis. Depois, identifique as consoantes e as vogais. Por fim, conte quantos anagramas começam e terminam com consoantes.
- Total de anagramas da palavra HOSPITAL:
\[ 8! = 40.320. \] - Vogais: O, I, A (3 letras). Consoantes: H, S, P, T, L (5 letras).
- Número de anagramas com início e fim em consoante:
\[ 5 \times 4 \times 6! \] - Probabilidade:
\[ \frac{5 \times 4 \times 6!}{8!} = \frac{20 \times 720}{40.320} = \frac{14.400}{40.320} = \frac{20}{56} = \frac{5}{14}. \]
✅ RESPOSTA CORRETA:
Alternativa A) \(\frac{5}{14}\)
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão
Questão 10
(UPE SSA 3 - 2016) Selecionamos ao acaso duas arestas do prisma triangular regular representado abaixo.

Qual é a probabilidade de elas não serem paralelas?
Primeiro, conte o total de arestas do prisma triangular regular. Depois, identifique quantos pares de arestas são paralelas. Por fim, calcule a probabilidade complementar (1 - probabilidade de serem paralelas).
- Total de arestas em um prisma triangular regular: 9 (3 nas bases e 6 laterais).
- Total de pares de arestas:
\[ C(9,2) = \frac{9 \times 8}{2} = 36 \] - Pares de arestas paralelas:
- 3 pares nas bases (arestas correspondentes)
- 3 pares nas arestas laterais
Total: 6 pares paralelos - Probabilidade de não serem paralelas:
\[ 1 - \frac{6}{36} = \frac{30}{36} = \frac{5}{6} \]
✅ RESPOSTA CORRETA:
Alternativa E) \(\frac{5}{6}\)
Vídeo gabarito:
O vídeo gabarito ainda não está disponível para essa questão

\(\textbf{Passo 1:}\) Identificar o total de alunas (mulheres) nas três turmas
Da tabela temos:
\[ \text{Total de alunas} = 28 + 24 + 32 = 84 \]
\(\textbf{Passo 2:}\) Identificar o número de alunas da turma A
\[ \text{Alunas da turma} A=28 \]
\(\textbf{Passo 3:}\) Calcular a probabilidade de escolher uma aluna da turma A
\[ P(\text{turma A}) = \frac{28}{84} = \frac{1}{3} \]
✅ RESPOSTA CORRETA:
Alternativa B) \(\frac{1}{3}\)