A Figura apresenta a disposição de 20 carteiras escolares em uma sala de aula. As carteiras que estão identificadas por letras já estavam ocupadas quando Marcelo, Joana e Clara entraram na sala.

Se Marcelo, Joana e Clara vão escolher três carteiras seguidas (lado a lado), de quantos modos distintos eles podem sentar-se?
🎓 Dica do Professor:
Preste atenção! O segredo desta questão está em visualizar os "blocos" de três carteiras vagas e consecutivas que podem ser formados na sala. Primeiro, identifique todas as fileiras (horizontais e verticais) onde é possível encaixar um grupo de três pessoas lado a lado. Depois, para cada um desses blocos de carteiras, lembre-se de que as três pessoas podem se permutar entre si, ocupando as mesmas três carteiras de maneiras diferentes.
Certa operadora de telefonia celular oferece diferentes descontos na compra de aparelhos, dependendo do plano contratado pelo cliente. A Tabela a seguir apresenta os percentuais de desconto oferecidos na compra do aparelho X que, sem desconto, custa p reais.

Lucas contratou o Plano 1, Gabriel, o Plano 2 e Carlos, o Plano 3, e os três adquiriram o aparelho X. Se Gabriel pagou, pelo aparelho X, R$ 120,00 a menos do que Lucas, o desconto obtido por Carlos, em reais, foi de
🎓 Dica do Professor:
O segredo aqui é encontrar o preço original \(p\) do aparelho. A diferença de preço paga por Gabriel e Lucas (R$ 120,00) é resultado da diferença entre seus descontos (40% e 15%). Encontre \(p\) usando essa informação. Depois, basta aplicar o desconto de Carlos (80%) sobre esse preço p para encontrar o valor do desconto em reais.
1. Identificação das Informações e Definição de Variáveis:
- O preço original do aparelho é \( p \) reais.
- Plano 1 (Lucas): Desconto de 15%, preço pago \( = p - 0,15p = 0,85p \).
- Plano 2 (Gabriel): Desconto de 40%, preço pago \( = p - 0,40p = 0,60p \).
- Plano 3 (Carlos): Desconto de 80%, preço pago \( = p - 0,80p = 0,20p \).
2. Diferença entre o preço pago por Gabriel e Lucas:
A questão nos diz que Gabriel pagou R$ 120 a menos que Lucas. Isso implica que:
\[ 0,85p - 0,60p = 120 \]
Simplificando:
\[ 0,25p = 120 \]
Logo, o preço original do aparelho é:
\[ p = \frac{120}{0,25} = 480 \]
3. Cálculo do Desconto de Carlos:
Agora que sabemos que o preço original do aparelho é \( p = 480 \) reais, podemos calcular o valor que Carlos pagou, aplicando o desconto de 80%:
O preço pago por Carlos é:
\[ 0,20 \times 480 = 96 \]
Portanto, o desconto obtido por Carlos foi:
\[ 480 - 96 = 384 \]
Portanto, a resposta correta é a alternativa D.
Durante um ano, Eduardo efetuou um depósito por mês em sua conta poupança. A cada mês, a partir do segundo, Eduardo aumentou o valor depositado em R$ 15,00, em relação ao mês anterior.
Se o total por ele depositado nos dois últimos meses foi R$ 525,00, quantos reais Eduardo depositou no primeiro mês?
🎓 Dica do Professor:
Este problema trata-se de uma Progressão Aritmética (P.A.), onde cada termo aumenta um valor fixo em relação ao anterior. Represente o valor do depósito do 11º e do 12º mês usando a fórmula do termo geral \(a_n = a_1 + (n-1) \cdot r\). A soma desses dois termos é igual a 525. Isso formará uma equação linear simples para encontrar o primeiro termo \(a_1\).
Passo 1: Definir a Progressão (P.A.)
Seja:
- \(a_1\): o valor do primeiro depósito (o que queremos encontrar).
- \(r = 15\): a razão da P.A. (aumento mensal).
- \(n = 12\): o número total de meses (termos).
Passo 2: Escrever os termos dos dois últimos meses
Usando a fórmula do termo geral de uma P.A., \(a_n = a_1 + (n-1) \cdot r\):
11º mês (penúltimo): \( a_{11} = a_1 + (11-1) \cdot 15 = a_1 + 10 \cdot 15 = a_1 + 150 \)
12º mês (último): \( a_{12} = a_1 + (12-1) \cdot 15 = a_1 + 11 \cdot 15 = a_1 + 165 \)
Passo 3: Montar a equação com a informação do problema e determinar a_1
A soma dos dois últimos meses é R$ 525,00:
\[ a_{11} + a_{12} = 525 \]
\[ (a_1 + 150) + (a_1 + 165) = 525 \]
\[ 2 \cdot a_1 + 315 = 525 \]
\[ 2 \cdot a_1 = 525 - 315 \]
\[ 2 \cdot a_1 = 210 \]
\[ a_1 = \frac{210}{2} = 105 \]
Portanto, Eduardo depositou R$ 105,00 no primeiro mês. Gabarito: B
Dentro de uma gaveta há garfos, facas e colheres, totalizando 48 talheres. A soma das quantidades de garfos e de facas corresponde ao dobro da quantidade de colheres. Se fossem colocadas mais 6 facas dentro dessa gaveta, e nenhuma colher fosse retirada, a quantidade de facas se igualaria à de colheres.
Quantos garfos há nessa gaveta?
🎓 Dica do Professor:
O segredo é traduzir as informações do problema em equações. Chame a quantidade de garfos de \(G\), facas de \(F\) e colheres de \(C\). Você terá três informações que formarão um sistema de três equações. Use a última informação ("se fossem colocadas mais 6 facas...") para encontrar uma relação simples entre \(F\) e \(C\). Substitua nas outras equações e descubra o valor de \(G\).
Passo 1: Definir as variáveis
Sejam:
- \(G\): número de garfos
- \(F\): número de facas
- \(C\): número de colheres
Passo 2: Montar o sistema de equações
Do enunciado, temos:
(1) \( G + F + C = 48 \) (Total de talheres)
(2) \( G + F = 2C \) (Soma de garfos e facas é o dobro das colheres)
(3) \( F + 6 = C \) (Com mais 6 facas, facas igualam às colheres)
Passo 3: Resolver o sistema
Substituindo a equação (3) na equação (2):
\[ G + F = 2(F + 6) \]
\[ G + F = 2F + 12 \]
\[ G = F + 12 \quad \text{(4)} \]
Agora, substitua a equação (3) e a equação (4) na equação (1):
\[ (F + 12) + F + (F + 6) = 48 \]
\[ 3F + 18 = 48 \]
\[ 3F = 30 \]
\[ F = 10 \]
Passo 4: Encontrar o número de garfos (\(G\))
Substituindo \(F = 10\) na equação (4):
\[ G = 10 + 12 \]
\[ G = 22 \]
Portanto, há 22 garfos na gaveta. Gabarito: E
Qual é o produto das raízes da equação
\[ \left[ \log \left( x \right) \right]^{2} \,\, - \,\, \log \left( x^2 \right) \,\, - \,3 \, = 0 \]
🎓 Dica do Professor:
Para resolver essa equação, utilize a propriedade dos logaritmos \(\log(x^2) = 2 \cdot \log(x)\) para simplificar a equação. Faça uma mudança de variável considerando \(y = \log(x)\). Em seguida, resolva a equação quadrática resultante e encontre as raízes. Não se esqueça de substituir de volta para a variável \(x\).
A equação dada é:
\[ \left[ \log \left( x \right) \right]^2 - \log \left( x^2 \right) - 3 = 0 \]
Passo 1: Simplificar \(\log(x^2)\) utilizando a propriedade dos logaritmos:
\[ \log(x^2) = 2 \cdot \log(x) \]
Substituindo na equação, temos:
\[ \left[ \log(x) \right]^2 - 2 \cdot \log(x) - 3 = 0 \]
Passo 2: Substituir \( y = \log(x) \):
\[ y^2 - 2y - 3 = 0 \]
Passo 3: Resolver a equação quadrática \( y^2 - 2y - 3 = 0 \) utilizando a fórmula de Bhaskara:
\[ y = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(-3)}}{2(1)} \]
\[ y = \frac{2 \pm \sqrt{4 + 12}}{2} \]
\[ y = \frac{2 \pm \sqrt{16}}{2} \]
\[ y = \frac{2 \pm 4}{2} \]
Portanto, as soluções para \(y\) são:
\[ y_1 = 3 \quad \text{e} \quad y_2 = -1 \]
Passo 4: Voltar para \(x\), temos:
\[ \log(x_1) = 3 \quad \Rightarrow \quad x_1 = 1000 \]
\[ \log(x_2) = -1 \quad \Rightarrow \quad x_2 = 0,1 \]
Passo 5: O produto das raízes é:
\[ x_1 \times x_2 = 1000 \times 0,1 = 100 \]
Portanto, o produto das raízes é \(100\).
Um cilindro circular reto possui altura igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em metros cúbicos, e a sua área total, dado em metros quadrados, é igual a 2 metros, então a área lateral do cilindro, em m², é igual a:
🎓 Dica do Professor:
Neste problema, a chave é perceber que a altura do cilindro é igual ao raio da base, o que simplifica as fórmulas. Use a informação da razão entre o volume e a área total do cilindro para encontrar o raio, e então calcular a área lateral.
Sabemos que a altura do cilindro é igual ao raio da base, ou seja, \(h = r\).
Passo 1: Fórmulas que vamos utilizar:
- Volume do cilindro:
\[ V = \pi r^2 h = \pi r^3 \]
- Área total do cilindro:
\[ A_{\text{total}} = 2\pi r^2 + 2\pi r h = 4\pi r^2 \]
- Razão entre o volume e a área total:
\[ \frac{V}{A_{\text{total}}} = 2 \]
Substituindo as expressões para \(V\) e \(A_{\text{total}}\):
\[ \frac{\pi r^3}{4\pi r^2} = 2 \]
Simplificando:
\[ \frac{r}{4} = 2 \]
Multiplicando ambos os lados por 4:
\[ r = 8 \]
Passo 2: Calcular a área lateral:
A área lateral do cilindro é dada por:
\[ A_{\text{lateral}} = 2\pi r h = 2\pi r^2 \]
Substituindo \(r = 8\):
\[ A_{\text{lateral}} = 2\pi (8)^2 = 2\pi \times 64 = 128\pi \]
Portanto, a área lateral do cilindro é \(128\pi\) metros quadrados.
Um laboratório farmacêutico precisa transferir 240 litros de vacina para ampolas de 15 cm³ de capacidade cada, enchendo-as completamente.
Considerando-se essas informações, quantas ampolas serão utilizadas para essa transferência?
Dado: 1 dm³ corresponde a 1 litro
🎓 Dica do Professor:
Lembre-se de que \(1 \, \text{litro} = 1000 \, \text{cm}^3\). Então, ao trabalhar com volumes em litros e ampolas em cm³, você deve convertir os litros para cm³ antes de calcular o número de ampolas necessárias.
Sabemos que:
\[ 1 \, \text{litro} = 1 \text{dm}^3 = 1000 \, \text{cm}^3 \]
Portanto, a quantidade de vacina em cm³ é:
\[ 240 \, \text{litros} = 240 \times 1000 = 240.000 \, \text{cm}^3 \]
Agora, cada ampola tem capacidade de \(15 \, \text{cm}^3\). O número de ampolas necessárias é:
\[ \frac{240.000 \, \text{cm}^3}{15 \, \text{cm}^3} = 16.000 \]
Logo, o número de ampolas que serão utilizadas para a transferência é \(16.000\).
Um laboratório possui dois recipientes de vidro. O primeiro recipiente tem a forma de uma esfera cujo raio mede R metros, e o segundo tem a forma de um cone, cujo raio da base e cuja altura medem R metros.
A razão entre a medida do volume do recipiente esférico e a medida do volume do recipiente cônico, ambas dadas em metros cúbicos, é
🎓 Dica do Professor:
Relembre as fórmulas de volume dos sólidos. Para a esfera: \(V_{\text{esfera}} = \frac{4}{3}\pi R^3\). Para o cone: \(V_{\text{cone}} = \frac{1}{3}\pi R^2 h\). No problema, a altura do cone é igual ao raio da base (\(h = R\)), o que simplifica muito o cálculo. Substitua os valores e simplifique a razão entre os volumes.
Passo 1: Volume da esfera
O volume de uma esfera de raio \(R\) é dado by:
\[ V_{\text{esfera}} = \frac{4}{3} \pi R^3 \]
Passo 2: Volume do cone
O volume de um cone de raio da base \(R\) e altura \(h\) é:
\[ V_{\text{cone}} = \frac{1}{3} \pi R^2 h \]
Como a altura também mede \(R\) metros (\(h = R\)), temos:
\[ V_{\text{cone}} = \frac{1}{3} \pi R^2 \cdot R = \frac{1}{3} \pi R^3 \]
Passo 3: Calcular a razão
A razão entre o volume da esfera e o volume do cone é:
\[ \text{Razão} = \frac{V_{\text{esfera}}}{V_{\text{cone}}} = \frac{\frac{4}{3} \pi R^3}{\frac{1}{3} \pi R^3} \]
Passo 4: Simplificar a expressão
Cancelando os termos comuns \(\pi\) e \(R^3\):
\[ \text{Razão} = \frac{\frac{4}{3}}{\frac{1}{3}} = \frac{4}{3} \times \frac{3}{1} = 4 \]
Portanto, a razão entre os volumes é 4. Gabarito: C
Para b ∈ R, considere a equação \(2x + b = x^2 - 2x - 4\).
A equação dada possui 2 raízes reais distintas quando, e apenas quando,
🎓 Dica do Professor:
Para que uma equação quadrática tenha duas raízes real e distintas, o discriminante (\(\Delta\)) deve ser estritamente positivo. Comece reorganizando a equação dada para a forma padrão \(ax^2 + bx + c = 0\). Em seguida, calcule \(\Delta = b^2 - 4ac\) e imponha a condição \(\Delta > 0\). Isso resultará em uma desigualdade envolvendo o parâmetro \(b\).
Passo 1: Reorganizar a equação na forma padrão
A equação dada é:
\[ 2x + b = x^2 - 2x - 4 \]
Subtraindo \(2x + b\) de ambos os lados:
\[ 0 = x^2 - 2x - 4 - 2x - b \]
\[ 0 = x^2 - 4x - (4 + b) \]
Portanto, a equação na forma \(ax^2 + bx + c = 0\) é:
\[ x^2 - 4x - (4 + b) = 0 \]
Onde:
\( a = 1 \)
\( b_{\text{coef}} = -4 \)
\( c = -(4 + b) \)
Passo 2: Calcular o discriminante \(\Delta\)
\[ \Delta = (b_{\text{coef}})^2 - 4ac = (-4)^2 - 4 \cdot 1 \cdot [-(4 + b)] \]
\[ \Delta = 16 + 4(4 + b) = 16 + 16 + 4b = 32 + 4b \]
Passo 3: Impor a condição para duas raízes reais distintas
Para duas raízes reais distintas, \(\Delta > 0\):
\[ 32 + 4b > 0 \]
Passo 4: Resolver a inequação
\[ 4b > -32 \]
\[ b > -8 \]
Portanto, a equação possui duas raízes reais distintas se e somente se \(b > -8\). Gabarito: B
Três herdeiros, Arnaldo, Bruno e Paulo, dividiram um terreno quadrado de 42 metros de lado em três terrenos retangulares de áreas iguais. A Figura abaixo mostra a divisão e a parte que coube a cada um.
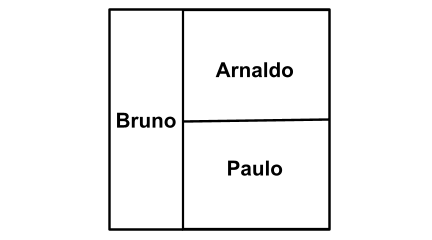 O perímetro, em metros, do terreno retangular destinado a Bruno é
O perímetro, em metros, do terreno retangular destinado a Bruno é
🎓 Dica do Professor:
A chave é usar a informação de que as três áreas são iguais. Use a fórmula da área do quadrado para encontrar a área do terreno. Cada herdeiro recebe um terço da área do terreno. Use a área conhecida e as relações entre os lados do quadrado para encontrar as dimensões do retângulo de Bruno. Com as dimensões, calcule o perímetro.
Passo 1: Calcular a área total e a área de cada parte
O terreno é um quadrado de lado 42 m:
\[ \text{Área}_{\text{total}} = 42 \times 42 = 1764 \, \text{m}^2 \]
Cada herdeiro recebe um terreno de área igual:
\[ \text{Área}_{\text{cada}} = \frac{1764}{3} = 588 \, \text{m}^2 \]
Passo 2: Deduzir as dimensões dos retângulos
Observe na figura que as dimensões do terreno de Bruno são \( 42 m \times x m\) e, pela divisão, esse terreno tem 588 m². Logo,
\[ 42 \times x = 588 \implies x = \frac{588}{42} = 14 \, \text{m} \]
Passo 3: Calcular o perímetro do retângulo de Bruno
O retângulo de Bruno tem dimensões 42 m por 14 m. Seu perímetro \(P\) é:
\[ P = 2 \times (\text{largura} + \text{altura}) = 2 \times (42 + 14) = 2 \times 56 = 112 \, \text{m} \]
Portanto, o perímetro do terreno de Bruno é \(112 m\). Gabarito: D

Como temos 3 pessoas que vão sentar-se lado a lado, eles só podem se sentar na fileira horizontal central e, há apenas 2 casos possíveis como você pode observar na figura abaixo:
Em cada um dos casos as 3 pessoas podem permutar entre si, de forma que para cada uma dos casos, temos:
\[ P_{3} = 3! = 3 \cdot 2\cdot 1 = 6 \]
Logo, Marcelo, Joana e Clara podem optar pelas carteiras do caso 1 ou caso 2 tendo, em cada caso, 6 possibilidades resultando em um total de:
\[ 2 \times 6 = 12 \text{ possibilidades} \]
Portanto, a resposta correta é a alternativa C.