As provas foram aplicadas pela banca FGV nas datas: 23 de março, 30 de março, 6 de abril e 13 de abril de 2025 e os resultados já foram divulgados os resultados definitivos da etapa objetiva do concurso da Prefeitura de Canaã dos Carajás, localizada no estado do Pará.
O edital oferta 556 vagas em diversos cargos, distribuídos em todos os níveis de escolaridade, com salários que vão de R$ 1.610,36 até R$ 11.760,99.
Ao todo, foram 48.685 inscritos para os diversos cargos contemplados, sendo que o mais procurado foi para Agente de Serviços Técnicos em Enfermagem (107,07 x vaga).
Conteúdos
Concurso Canaã dos Carajás: etapas de provas
O certame é constituído das seguinte etapas de avaliação:
- Prova objetiva: para todos os cargos de caráter eliminatório e classificatório;
- Prova Dissertativa: para os cargos de Nível Superior de Procurador Municipal e para os cargos de Professor de caráter eliminatório e classificatório; e
- Prova de títulos: para todos os cargos de Nível Superior, de caráter classificatório;
Prova de Raciocínio Lógico Comentada
Questão 1
Considere dois conjuntos numéricos finitos A e B tais que:
• \(A \cup B = \left\{ 2, 3, 4, 5 \right\}\)
• \(A \cap B = \left\{ 2 \right\}\)
Com base nessas informações, é correto afirmar que:
\(\textbf{1. Pense na interseção como o "ponto em comum" e na união como "todos os elementos juntos"}\).
\(\textbf{2. Tente distribuir os elementos que sobraram (3, 4, 5) entre A e B sem repetir.}\)
\(\textbf{3. Veja se é possível que ambos tenham o mesmo número de elementos.}\)
Questão 2
Marcelo participa de um jogo em que, a cada rodada, ele aposta todo o dinheiro que tem, havendo apenas duas possibilidades: ganhar a rodada ou perdê-la. Em caso de vitória na rodada, o jogador recebe de volta o dobro do que apostou. Em caso de derrota na rodada, recebe de volta a metade. Se Marcelo começou com R$ 10,00, depois de participar de 2 rodadas, ele deverá ter:
Questão 3
Um grupo é formado por, exatamente, 9 crianças com idades no intervalo que vai de 10 anos a 13 anos (incluídos esses dois valores).
É certo que, entre essas crianças,
\(\textbf{Pense no princípio das gavetas (ou princípio da casa dos pombos)!}\)
\(\textbf{Se temos poucas gavetas (as idades possíveis) e muitos pombos (as crianças), alguma idade será repetida mais de uma vez}.\)
\(\textbf{Tente distribuir as 9 crianças sem que três fiquem com a mesma idade — você verá que não é possível.}.\)
\(\textbf{🗂️ Assunto: Princípio das casas dos pombos.}\)
\(\textbf{\(\triangleright\)\(\,\,\) As idades possíveis são: 10, 11, 12 e 13. Logo, temos 4 idades distintas.}\)
\(\textbf{\(\triangleright\)\(\,\,\) Temos 9 crianças para distribuir nessas 4 idades.}\)
\(\textbf{Se quisermos evitar que alguma idade tenha 3 ou mais crianças, no máximo podemos colocar 2 crianças em cada idade.}\)
\(\textbf{Distribuindo o máximo possível sem atingir 3 por idade:}\)
\(\textbf{\(\bullet\)\(\,\,\) Idades 10 anos \(\,\, \to \,\,\) Duas criânças.}\)
\(\textbf{\(\bullet\)\(\,\,\) Idades 11 anos \(\,\, \to \,\,\) Duas criânças.}\)
\(\textbf{\(\bullet\)\(\,\,\) Idades 12 anos \(\,\, \to \,\,\) Duas criânças.}\)
\(\textbf{\(\bullet\)\(\,\,\) Idades 13 anos \(\,\, \to \,\,\) Duas criânças.}\)
\[ \textbf{4 \(\times\) 2 = 8 \(\text{crianças}\)} \] \(\textbf{Só conseguimos acomodar 8 crianças colocando no máximo 2 por idade.}\)
\(\textbf{ Como temos 9 crianças, uma delas ficará em uma idade que já possui 2 crianças, formando assim um grupo de 3.}\)
\(\textbf{Portanto, pelo menos três crianças têm a mesma idade.}\)
Questão 4
Em uma planta baixa, a representação de uma casa corresponde a um retângulo de lados 6 cm e 9 cm. Uma parte dentro da casa, também retangular, foi destinada à cozinha.
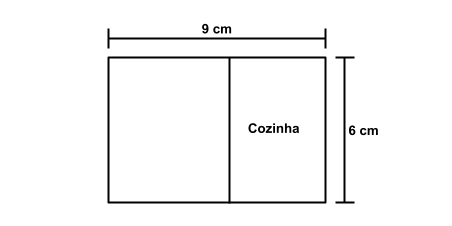
Sabendo-se que os retângulos ocupados pela cozinha e pela casa são semelhantes, conclui-se que, na planta baixa, o perímetro do retângulo que representa a cozinha tem:
Lembre-se de que, em figuras semelhantes, os lados correspondentes são proporcionais. Você já conhece um lado da cozinha (6 cm), basta encontrar o outro usando a razão de semelhança e depois calcular o perímetro.
\(\textbf{Assunto: Semelhança de figuras planas (razão de semelhança e perímetro).}\)
\(\textbf{1º A casa tem lados 6 cm (menor) e 9 cm (maior).}\)
\(\textbf{A cozinha é semelhante à casa e possui um lado de 6 cm.}\)
\(\textbf{Como os retângulos são semelhantes, temos:}\)
\[ \frac{6}{9} = \frac{y}{6} \]
\(\textbf{Isolando} \)\(y\):
\[ y = \frac{6 \times 6}{9} = \frac{36}{9} = 4 \;\text{cm} \]
\(\textbf{Assim, os lados da cozinha são 6 cm e 4 cm.}\)
\(\textbf{Perímetro da cozinha:}\)
\[ 2 \times (6 + 4) = 2 \times 10 = 20 \;\text{cm} \]
Questão 5
Três objetos são capazes de manter as suas temperaturas inalteradas, a não ser que sejam colocados em contato entre si. Nesse caso, os objetos em contato transferem calor entre si até que todos fiquem com a mesma temperatura.
Os corpos são:
• A, inicialmente com temperatura de 70 °C;
• B, inicialmente com temperatura de 66 °C;
• C, inicialmente com temperatura de 56 °C.
O corpo A é posto em contato com o corpo B e, depois de alcançado o equilíbrio entre esses dois corpos, o corpo B é posto em contato com o corpo C, até que se atinja o equilíbrio entre eles.
Não há qualquer outro contato entre os corpos.
Após o segundo equilíbrio, a temperatura do corpo A é
\(\textbf{Pense em cada etapa de equilíbrio separadamente!}\)
\(\textbf{Primeiro, encontre a temperatura de equilíbrio entre A e B.}\)
\(\textbf{Depois, considere que A fica isolado e B entra em contato com C.}\)
\(\textbf{Primeiro equilíbrio (A com B):}\)
\(\textbf{Temperaturas iniciais:} \;\; A = 70 \; ^\circ\mathrm{C}, \;\;B = 66 \; ^\circ\mathrm{C}.\)
\[ T_{média_{AB}} = \frac{70 + 66}{2} = 68 \; ^\circ\mathrm{C} \]
\(\textbf{Segundo equilíbrio (B com C):}\)
\(\textbf{Então o corpo B, que agora tem \(68 \; ^\circ\mathrm{C}\), é colocado em contato com o corpo C (\(56 \; ^\circ\mathrm{C}\)).}\)
\(\textbf{Calculando a média:}\)
\[ T_{média_{BC}} = \frac{68 + 56}{2} = 62 \; ^\circ\mathrm{C} \]
\(\textbf{Após isso:}\)
A = 68 °C
B = 62 °C
C = 62 °C
\(\textbf{Comparando A e B:}\)
\[ 68 - 62 = 6 \; ^\circ\mathrm{C} \]
\(\textbf{Resposta:A está 6 °C mais quente que B.} \)
\(\textbf{Alternativa correta: C.}\)
Questão 6
Sandro realiza um programa de redução de tabagismo. As quantidades de cigarros fumados diariamente por ele nos últimos 5 dias da semana estão indicadas a seguir.
• terça-feira: 16 cigarros;
• quarta-feira: 14 cigarros;
• quinta-feira: 12 cigarros;
• sexta-feira: 10 cigarros;
• sábado: 13 cigarros.
O seu consumo médio de cigarros nesse período foi
\(\textbf{Para calcular a média, some todos os valores e divida pela quantidade de dias. Depois, compare o valor encontrado com cada alternativa.}\)
\(\textbf{Soma das quantidades de cigarros fumados diariamente por Sandro:}\) \[ \textbf{16 + 14 + 12 + 10 + 13 = 65} \]
\(\textbf{Número de dias:}\) \[ \textbf{5} \]
\(\textbf{Cálculo da média:}\)
\[ \textbf{\(\frac{65}{5} = 13\)} \]
\(\textbf{Comparação com os valores diários:}\)
\(\textbf{Terça-feira: 16 (maior que 13)}\)
\(\textbf{Quarta-feira: 14 (maior que 13)}\)
\(\textbf{Quinta-feira: 12 (menor que 13)}\)
\(\textbf{Sexta-feira: 10 (menor que 13)}\)
\(\textbf{Sábado: 13 (igual à média)}\)
\(\textbf{Resposta: C) menor do que a quantidade consumida na quinta-feira.}\)
Questão 7
Uma certa quantidade de dinheiro foi dividida em duas partes diretamente proporcionais a 1 e 2 e submetidas a diferentes rentabilidades pelo mesmo intervalo de tempo, o que fez com que ambas aumentassem de valor.
A parte menor teve rentabilidade de 50% enquanto a maior rendeu 20%. Com isso, o valor total resgatado foi de R$ 780,00.
Se as duas partes iniciais tivessem exatamente os mesmos valores, mas as rentabilidades fossem trocadas, o valor total resgatado seria
\(\textbf{Divida o valor inicial em partes proporcionais a 1 e 2, depois aplique as porcentagens de rendimento.}\) \(\textbf{Em seguida, troque as porcentagens e compare os novos valores resgatados.}\)
\(\textbf{Vamos representar as partes!!}\)
Como o dinheiro foi dividido em duas partes diretamente proporcionais a 1 e 2, então uma parte será o dobro da outra.
Vamos chamá-las de \(x\) e \(2x\).
Vamos representar os rendimentos de cada uma das duas partes:
\(\textbf{A menor parte (x) rendeu 50%. \(\to\) 150% de x.}\)
\(\textbf{A maior parte (2x) rendeu 20%. \(\to\) 120% de 2x.}\)
Sabemos que o valor total resgatado foi de R$ 780,00, teremos:
\[ 1,50 \cdot x+1,20 \cdot 2x = 780 \]
\[ 1,50\cdot x + 2,4 \cdot x = 780 \]
\[ 3,9x = 780 \quad \Longrightarrow \quad x = \frac{780}{3,9} = 200. \]
\(\textbf{Portanto, as partes eram de R$ 200,00 e R$ 400,00.}\)
\(\textbf{Troca das rentabilidades:}\)
\(\textbf{A menor parte (R$ 200,00) rendeu 20%. \(\to\) 120% de R$ 200,00.}\)
\(\textbf{A maior parte (R$ 400,00) rendeu 50%. \(\to\) 150% de R$ 400,00.}\)
\(\textbf{o valor total resgatado seria:}\)
\[ 120% de 200 + 150% de 400 \]
\[ = \frac{120}{100} \cdot 200 + \frac{150}{100} \cdot 400 \]
\[ = 120 \cdot 2 + 150 \cdot 4 \]
\[ = 240 + 600 = 840 \to R$ 840,00 \]
\(\textbf{Portanto a diferença do total resgatadoseria:}\)
\[ R$ 840,00 – R$ 780,00 = R$ 60,00. \]
\(\textbf{Resposta:} B) R$ 60,00 maior.\)
Questão 8
Em uma sacola, há 12 mangas. Sabe-se que, infelizmente, 3 delas estão estragadas.
Se duas mangas forem sorteadas ao acaso, a probabilidade de que uma delas esteja estragada e a outra não, é de
Lembre-se: Quando pedimos uma probabilidade de "uma estragada e uma boa", podemos usar combinações para contar as formas favoráveis e o total de maneiras de escolher 2 mangas.
\(\textbf{1. Total de mangas:}\)
Total = 12, Estragadas = 3, Boas = 12 - 3 = 9.
\(\textbf{2. Total de maneiras de escolher 2 mangas:}\)
\[ \binom{12}{2} = \frac{12 \times 11}{2} = 66. \]
\(\textbf{3. Número de maneiras de escolher 1 estragada e 1 boa:}\)
\[ \binom{3}{1} \times \binom{9}{1} = 3 \times 9 = 27. \]
\(\textbf{4. Probabilidade:}\)
\[ P = \frac{27}{66} = \frac{9}{22}. \]
\(\textbf{Resposta:} A) \frac{9}{22}.\)
Questão 9
Considere, no plano cartesiano, os pontos A (1,2) e B (5,2).
Assinale a opção que indica um ponto do plano cartesiano que equidista dos pontos A e B.
Quando um ponto equidista de outros dois, ele está na mediatriz do segmento que os une. Para pontos no plano, essa mediatriz é a reta perpendicular ao segmento AB que passa pelo ponto médio de AB.
\(\textbf{Assunto:} Geometria Analítica — Ponto médio e mediatriz.\)
\(\textbf{1. Ponto médio de AB:}\)
\[ M = \left(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2}\right) = \left(\frac{1+5}{2}, \frac{2+2}{2}\right) = (3, 2). \]
\(\textbf{2. Mediatriz:}\)
O segmento AB é horizontal (mesma ordenada). Sua mediatriz é a reta vertical que passa por \(x = 3\).
\(\textbf{3. Verificação:}\)
O único ponto dado que possui \(x = 3\) é o ponto (3,7).
\(\textbf{Conclusão:}\)
\[ \text{Ponto equidistante: } (3,7). \]
\(\textbf{Resposta:} D) (3,7).\)
Questão 10
Considere um número inteiro par. Se o seu dobro for somado à sua metade, o resultado é, certamente, um múltiplo de
Comece representando o número par como \(2n\). Depois, calcule seu dobro e sua metade e veja como fica a soma.
\(\textbf{Resolução passo a passo:}\)
\(\textbf{1. Representação do número:}\)
Seja \(2n\), com \(n \in \mathbb{Z}\).
\(\textbf{2. Dobro e metade:}\)
\[ \text{Dobro: } 2 \times (2n) = 4n. \]
\[ \text{Metade: } \frac{2n}{2} = n. \]
\(\textbf{3. Soma:}\)
\[ 4n + n = 5n. \]
\(\textbf{4. Conclusão:}\)
\[ 5n \text{ é sempre múltiplo de 5}. \]
\(\textbf{Resposta: C) 5.}\)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

\(\textbf{Sabemos que:}\)
\[ \textbf{A ∪ B = {2, 3, 4, 5} e A ∩ B = {2}}. \] \(\textbf{Logo, \(\text{2 \(\in\) A e 2 \(\in\) B}\). Os elementos 3, 4 e 5 devem ser distribuídos sem repetição.}\)
\(\textbf{Vamos analisar as alternativas:}\)
\(\textbf{A) um dos conjuntos é necessariamente vazio.}\)
\(\color{Red} {❌ Errado.}\)
\(\textbf{Como \(\text{2 \(\in\) A e 2 \(\in\) B}\), então A \(\neq \emptyset\) e B \(\neq \emptyset\).}\)
\(\textbf{B) um dos conjuntos é necessariamente unitário.}\)
\(\color{Red} {❌ Errado.}\)
\(\textbf{Observe o diagrama abaixo que apresenta um contraexemplo.}\)
\(\color{Red} {❌ Errado.}\)
\(\textbf{Chamemos os elementos X o conjunto dos elementos exclusivos de A e de Y o conjunto dos elementos exclusivos de A. Assim:}\)
\[ \textbf{A = \{2\} \(\cup\) X} \] \[ \textbf{ B = \{2\} \(\cup\) Y} \] \[ \textbf{ X \(\cup\) Y = \{3, 4, 5\}} \] \[ \textbf{X \(\cap\) Y = \(\emptyset\)} \] \(\textbf{Temos: }\) \[ \textbf{ n(A) = 1 + n(X) e n(B) = 1 + n(Y)} \] \[ \textbf{ n(X) + n(Y) = 3\(\,\,\,\) \(\to\)\(\,\,\,\) (1)} \] \(\textbf{ Para que A e B tenham a mesma quantidade de elementos: }\) \[ \textbf{ n(A) = n(B)} \] \[ \textbf{1 + n(X) = 1 + n(Y)} \] \[ \textbf{n(X) = n(Y)\(\,\,\,\) \(\to\)\(\,\,\,\) (2)} \] \(\textbf{Substituindo (2) em (1), temos:}\) \[ \textbf{n(X) + n(Y) = 3} \] \[ \textbf{n(X) + n(X) = 3} \] \[ \textbf{ 2 \(\cdot\) n(X) = 3} \] \[ \textbf{n(x) = \(\frac{3}{2}\) = 1,5} \]
\(\textbf{ o que não é possível. }\)
\(\textbf{ Portanto, A e B não podem ter o mesmo número de elementos. Eles sempre terão quantidades diferentes.}\)
\(\textbf{D) A e B têm quantidades diferentes de elementos.}\)
\(\color{Green} {✅ Correto.}\)
\(\textbf{Como vimos na análise anterior, A e B não podem ter a mesma quantidade de elementos.}\)