Futuro aluno do Instituto Federal de Alagoas (IFAL), quer arrasar na prova de Matemática? Aqui você encontrará a análise completa e detalhada do exame de seleção IFAL 2025, perfeita para você treinar, entender o exame e conquistar sua vaga!
Conteúdos
Comentário da prova de matemática IFAL 2025
Questão 1
Considere a expressão numérica:
\[
N = \sqrt{50} + 3 \cdot \sqrt{8} - 2\cdot \sqrt{18}
\]
Assinale a alternativa correta que contém o valor de N.
🎓 Dica do Professor:
Tente simplificar as raízes antes de realizar as operações. Procure escrever cada número dentro da raiz como produto de um quadrado perfeito e outro número. Por exemplo: \[ \sqrt{50} = \sqrt{25 \cdot 2} \] Isso vai te ajudar a juntar os radicais semelhantes!
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 2
Para os jogos internos de um colégio, foi criada uma competição para selecionar o melhor design de troféu para a premiação dos melhores colocados. Dois dos principais intuitos da competição é desenvolver o lado artístico dos alunos, mas também melhorar o conhecimento em geometria espacial, pois cada troféu deve ser formado por, ao menos, dois sólidos conhecidos. Maria participou da competição e elaborou o seguinte protótipo:
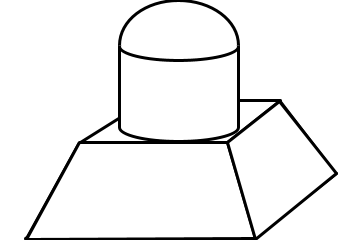
Assinale a alternativa que apresenta corretamente os sólidos que Maria utilizou para confeccionar seu protótipo.
🎓 Dica do Professor:
Observe bem a imagem e tente identificar as formas separadamente:
• O sólido da base tem formato de pirâmide ou cone?
• O do meio é um cilindro ou paralelepípedo?
• O do topo é uma esfera completa ou metade?
Compare com imagens de sólidos geométricos se necessário!
✍️ Comentário do professor:
Vamos analisar visualmente a imagem (caso o aluno esteja com ela aberta):1. Parte inferior (base):
É um tronco de pirâmide: tem uma base maior, uma base menor paralela a ela, e as faces laterais são trapézios. Isso mostra que a pirâmide foi "cortada", formando um tronco.
2. Parte intermediária (meio):
É um cilindro, pois apresenta base circular e superfície lateral curva, com as duas bases paralelas.
3. Parte superior (topo):
É uma semiesfera, pois se trata de "meia bola" perfeitamente encaixada sobre o cilindro.
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 3
No IFAL, os alunos do curso técnico em Agropecuária estão organizando uma horta comunitária. Eles sabem que, com 6 (seis) alunos trabalhando 5 horas por dia, durante 4 (quatro) dias, conseguem preparar 240 metros quadrados de terreno para plantio. Agora, os alunos precisam preparar uma nova área de 300 metros quadrados em apenas 2 (dois) dias, trabalhando o mesmo número de horas por dia. Assinale a alternativa que apresenta o número mínimo de alunos necessários para cumprir essa tarefa.
🎓 Dica do Professor:
Observe atentamente as informações dadas: há uma quantidade de alunos, uma carga horária diária, um número de dias e uma área que precisa ser preparada. Agora compare essa situação com a nova que envolve uma área diferente, menos dias disponíveis, mas mantendo a mesma carga horária.
Pergunte-se:
• Se a área a ser preparada aumentou, o que deve acontecer com a quantidade de alunos?
• Se o tempo disponível diminuiu, como isso afeta o esforço necessário?
• O que muda e o que permanece constante entre as duas situações?
Utilize esses questionamentos para organizar as grandezas em uma tabela e montar uma regra de três composta, analisando como cada fator influencia o total de alunos necessários.
✍️ Comentário do professor:
Vamos usar o raciocínio da regra de três composta, comparando duas situações.Situação 1 (inicial):
• 6 alunos
• 5 horas/dia
• 4 dias
• 240 m² preparados
Situação 2 (nova):
• x alunos
• 5 horas/dia (mesmo)
• 2 dias
• 300 m² a preparar
1º Passo: Vamos organizar os dados e aplicar a regra de três composta

Para analisar a relação de proporcionalidade entre as grandezas, vamos tomar com referência a área a ser preparada pelos alunos. (Podemos escolher qualquer grandeza como referência).

• O nº de alunos e a área são diretamente proporcionais: quanto mais alunos trabalhando, maior será a área preparada para o plantio.
• O nº de dias e a área são diretamente proporcionais: quanto maior o número de dias, maior será a área preparada para o plantio.
• O nº de horas/dias trabalhadas e a área são diretamente proporcionais: quanto maior o número horas/dia de trabalho, maior será a área preparada para o plantio.

2º Passo: Encontrar o valor de x.
\[ \frac{240}{300} = \frac{6}{x} \cdot \frac{5}{5} \cdot \frac{4}{2} \]
\[ \frac{240}{300} = \frac{120}{10 \cdot x} \]
\[ \frac{24}{30} = \frac{12}{x} \]
\[ 24 \cdot x = 30 \cdot 12 \]
\[ x = \frac{30 \cdot 12}{24} \]
Simplificando \[ x = \frac{30}{2} = 15 \]
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 4
Uma praça triangular é delimitada por uma ciclovia representada pelos segmentos AB, BC e AC. Deseja-se construir nela uma calçada para pedestres para evitar acidentes com as bicicletas que circulam na ciclovia. Essa calçada, representada na figura pelos segmentos CD, DE e EF, será construída de modo que os segmentos BC e DE sejam paralelos e os segmentos CD e EF sejam também paralelos.
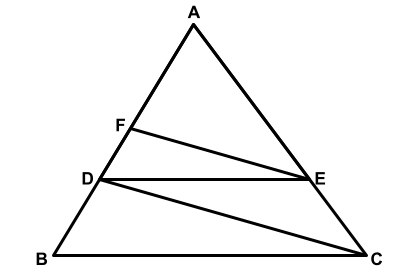
Sabendo-se que a extensão da ciclovia do ponto A até o ponto B mede 6,25 km e que a distância do ponto F até ponto A deve medir 2,56 km, assinale a alternativa que apresenta a distância correta do ponto A até o ponto D.
🎓 Dica do Professor:
Teorema Fundamental da semelhança
Quando um segmento de reta liga dois de um triângulo em pontos distintos, forma um triângulo que é semelhante ao primeiro. Observe a ilustração abaixo:
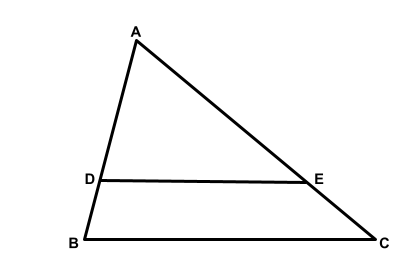
Na figura abaixo, representamos o triângulo ABC e o segmento DE paralelo ao lado BC.
\[
\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}
\]
Tente usar esse teorema no exercícios!
✍️ Comentário do professor:
1º Passo: Simplificando a figura como você vê abaixo, temos: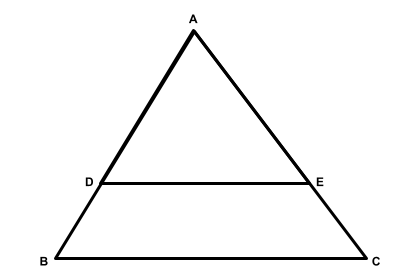
Os segmentos internos DE e BC são paralelos, portanto formam triângulos semelhantes.
\[ \frac{AD}{AB} = \frac{AE}{AC} \quad \text{(1)} \]
2º Passo: Simplificando a figura como você vê abaixo, temos:
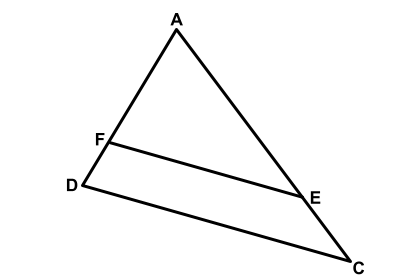
Os segmentos internos FE e DC são paralelos, portanto formam triângulos semelhantes.
\[ \frac{AF}{AD} = \frac{AE}{AC} \quad \text{(2)} \]
Observe que das igualdades (1) e (2), temos que:
\[ \frac{AD}{AB} = \frac{AF}{AD} \]
Agora é só aplicar a multiplicação cruzada.
\[ (AD)^2 = AB \cdot AF \] \[ (AD)^2 = 6,25 \cdot 2,56 \] \[ AD = \sqrt{6,25 \cdot 2,56} \] \[ AD = \sqrt{\frac{625}{100} \cdot \frac{256}{100}} \] \[ AD = \frac{25}{10} \cdot \frac{16}{10} = \frac{400}{100} = 4 \]
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 5
Considere o seguinte sistema de equações
\[
\begin{cases}
x^2 + y^2 = 25 \\
x + y = 7
\end{cases}
\]
Dadas as afirmativas,
I. Existem duas soluções para o sistema.
II. Não tem como resolver o sistema, pois uma equação envolve termos quadráticos e a outra não.
III. O problema em questão é um sistema de primeiro grau.
IV. O problema em questão é um sistema de equações do segundo grau.
verifica-se que estão corretas apenas
🎓 Dica do Professor:
Tente substituir uma equação na outra!
A equação \(x + y = 7\) pode ser usada para isolar uma das variáveis e substituir na outra equação. Isso ajuda a resolver o sistema mesmo que ele tenha uma equação com potência (segundo grau).
✍️ Comentário do professor:
Temos o sistema:\[ \begin{cases} x^2 + y^2 = 25 \quad \text{(1)} \\ x + y = 7 \quad \text{(2)} \end{cases} \] 1º Passo: Isolar uma variável na equação mais simples
A equação (2) é do 1º grau e mais fácil de manipular. Vamos isolar o \(y\):
\[ y = 7 - x \] 2º Passo: Substituir o valor de \(y\) na equação (1)
Substituímos \(y = 7 - x\) na equação (1):
\[ x^{2} + (7 − x)^{2} = 25 \] Agora, desenvolvemos o quadrado do binômio:
\[ x^{2} + (49 - 14x + x^{2}) = 25 \] \[ 2x^2 - 14x + 49 = 25 \] \[ 2x^2 - 14x + 24 = 0 \] Dividindo tudo por 2: \[ x^2 - 7x + 12 = 0 \] Agora, resolvemos usando a fórmula de Bhaskara:
Cálculo do \(\Delta\):
\[ \Delta = b^{2}-4 \cdot a \cdot c \] \[ \Delta = (-7)^{2}-4 \cdot 1 \cdot 12 \] \[ \Delta = 49 - 48 \] \[ \Delta = 1 \] Agora vamos usar a fórmula de Bhaskara:
\[ x = \frac{-b \pm \sqrt{\Delta}}{2 \cdot a} \] \[ x = \frac{-(-7) \pm \sqrt{1}}{2 \cdot 1} \] \[ x_{1} = \frac{7 + 1}{2} \Rightarrow x_{1} = \frac{8}{2} \Rightarrow x_{1} = 4 \] e \[ x_{2} = \frac{7 - 1}{2} \Rightarrow x_{2} = \frac{6}{2} \Rightarrow x_{2} = 3 \] Agora, calculamos os valores de \(y\):
Se \(x = 4\), então \(y = 3\)
Se \(x = 3\), então \(y = 4\)
✅ Conclusão:
• Existem duas soluções: (4,3) e (3,4) → Afirmativa I é correta
• O sistema pode ser resolvido → Afirmativa II é falsa
• O problema contém equação do 2º grau → Afirmativa III é falsa
• O problema é um sistema de equações do 2º grau → Afirmativa IV é correta
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 6
Uma construtora possui 30 metros quadrados de grama para construir um jardim de uma casa; porém, o cliente deu algumas exigências para a sua construção. Ele solicitou que a parte gramada tenha a forma de trapézio e, além disso, solicitou que a base maior desse trapézio seja 4 (quatro) metros maior que a altura dele, e a base menor 2 (dois) metros menor que a altura.
Diante dessas informações, a altura do trapézio que a construtora deverá entregar ao cliente, levando em consideração que serão plantados 30 metros quadrados de grama é de
🎓 Dica do Professor:
Lembre-se da fórmula da área do trapézio:
\[
A = \frac{(B + b) \cdot h}{2}
\]
Onde:
• A é a área,
• \(B\) é a base maior,
• \(b\) é a base menor,
• \(h\) é a altura.
Use as informações do problema para montar uma equação usando essa fórmula!
✍️ Comentário do professor:
1º Passo: Identificar as variáveisSeja \(h\) a altura do trapézio (o que queremos descobrir).
Segundo o problema:
• A base maior é 4 metros maior que a altura \(\to\) \(B = h + 4\)
• A base menor é 2 metros menor que a altura \(\to\) \(b = h - 2\)
• A área do trapézio é de 30 metros quadrados.
2º Passo: Substituir na fórmula da área do trapézio.
\[ A = \frac{(B + b) \cdot h}{2} \Rightarrow 30 = \frac{(h + 4 + h - 2) \cdot h}{2} \]
3º Passo: Simplificar a expressão.
\[ 30 = \frac{(2h + 2) \cdot h}{2} \] \[ 30 = \frac{2h^{2} + 2h}{2} \] \[ 30 = h^{2} + h \] \[ h^{2} + h - 30 = 0 \] Agora, resolvemos usando a fórmula de Bhaskara:
Cálculo do \(\Delta\):
\[ \Delta = b^{2}-4 \cdot a \cdot c \] \[ \Delta = (1)^{2}-4 \cdot 1 \cdot (-30) \] \[ \Delta = 1 + 120 \] \[ \Delta = 121 \] Agora vamos usar a fórmula de Bhaskara: \[ x = \frac{-b \pm \sqrt{\Delta}}{2 \cdot a} \] \[ x = \frac{-1 \pm \sqrt{121}}{2 \cdot 1} \] \[ x = \frac{-1 \pm 11}{2} \] \[ x_{1} = \frac{-1 + 11}{2} = \frac{10}{2} = 5 → (valor válido) \] \[ x_{2} = \frac{-1 - 11}{2} = \frac{-12}{2} = -6 → (valor inválido) \] ✅ Resposta correta: Letra B
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 7
A figura plana é um paralelogramo. Além disso, os ângulos BDC = CBA = 90° e \(\overline{AB} = 4\) e \(\overline{BF} = 5\).
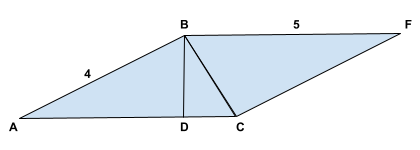
Assinale a alternativa que apresenta o valor correto de \(\overline{DC}\).
🎓 Dica do Professor:
Use a informação de que na figura têm ângulos de 90°, o que indica a possibilidade de termos triângulos retângulos e aplicar as relações métricas nos triângulos retângulos, entre elas o teorema de Pitágoras.
Identifique os triângulos retângulos corretamente para calcular o valor de \(\overline{DC}\).
✍️ Comentário do professor:
Vamos começar interpretando a figura.
Do enunciado temos que:
• AB = 4
• BF = 5
• \(\angle CBA\) = 90°
• \(\angle BDC\) = 90°
Com base nessas informaçoões podemos conluir que:
• O triângulo ABC é retângulo em B.
• O segmento \(\overline{BD}\) é a altura relativa a hipotenusa no triângulo ABC.Observe a figura abaixo:
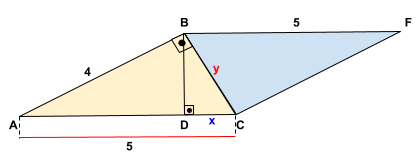
Na figura acima considere que \(\overline{BC}\) = y. Queremos determinar a medida \(\overline{DC}\) que vamos considerar como sendo igual a x.
Vamos começar determinando o valor de y. Para isso vamos aplicar o teorema de Pitágoras no triângulo ABC da figura acima.
\[
5^{2} = 4^{2} + y^{2}
\]
\[
25 = 16 + y^{2}
\]
\[
y^{2} = 25 - 16
\]
\[
y^{2} = 9
\]
\[
y = 3
\]
Agora vamos aplicar a relação métrica que relaciona a medida de um cateto com a medida de sua projeção sobre a hipotenusa com a propria hipotenusa.
\[
\left ( \overline{BC} \right )^{2} = \overline{DC} \cdot \overline{AC}
\]
\[
y^{2} = x \cdot 5
\]
\[
9 = x \cdot 5
\]
\[
x = \frac{9}{5}
\]
✅ Resposta correta: Letra A
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 8
Considere a expressão
\[
\frac{3x^{2} - 12x + 12}{6x^{2} - 18x + 12}
\]
A forma mais simplificada da expressão é
🎓 Dica do Professor:
Observe que tanto o numerador quanto o denominador são trinomiais quadrados.
• Coloque o fator comum em evidência:
\[
ax^2 + bx + c = a \cdot (x^2 + \cdots)
\]
• Verifique se pode aplicar:
\[
x^2 - 2ax + a^2 = (x - a)^2 \to \text{(quadrado da diferença)}
\]
• Ou use:
\[
x^2 + bx + c = (x - r_1) \cdot (x - r_2) \to (produto e soma das raízes)
\]
Depois, simplifique os fatores comuns entre numerador e denominador.
✍️ Comentário do professor:
Vamos começar fatorando as expressões no numerador e denominador.
Numerador:
\[
3x^{2} - 12x + 12 = 3 \cdot (x^{2} - 4x + 4) = 3 \cdot (x - 2)^2
\]
Denominador:
\[
6x^{2} - 18x + 12 = 6 \cdot (x^{2} - 3x + 2) = 6 \cdot (x - 1) \cdot (x - 2)
\]
Substitua as fatorações do numerador e denominador:
\[
\frac{3x^{2} - 12x + 12}{6x^{2} - 18x + 12} = \frac{3 \cdot (x - 2)^2}{6 \cdot (x - 1) \cdot(x - 2)} = \frac{3 \cdot (x - 2) \cdot (x-2)}{6 \cdot (x - 1) \cdot(x - 2)}
\]
Agora é só simplificar os coeficientes numéricos e também os fatores iguais que você encontrou nas fatorações do numerador e denominador:
\[
\frac{3x^{2} - 12x + 12}{6x^{2} - 18x + 12} = \frac{(x - 2)}{2 \cdot (x - 1)}
\]
Gabarito: Letra D
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 9
Considere o número 𝐿, dado pela seguinte expressão numérica
\[
L = \frac{\left( 3^{4} \cdot 9^{-1} \right)^{2}}{27^{\frac{2}{3}} \cdot 3^{-3}}.
\]
Assinale a alternativa que apresenta o valor correto de 𝐿.
🎓 Dica do Professor:
Use as propriedades de potências para transformar tudo em potências de mesma base.
• \(a^m \cdot a^n = a^{m+n}\)
• \((a^m)^n = a^{m \cdot n}\)
• \(\frac{a^m}{a^n} = a^{m - n}\)
• Lembre que \(9 = 3^2\) e \(27 = 3^3\)
✍️ Comentário do professor:
1º Passo: transformar todas as bases para base 3.Sabemos que:
\[ 9 = 3^2 \Rightarrow 9^{-1} = (3^2)^{-1} = 3^{-2} \] \[ 27 = 3^3 \Rightarrow 27^{\frac{2}{3}} = (3^3)^{\frac{2}{3}} = (3)^{3 \cdot \frac{2}{3}} = 3^{2}. \] Substituindo:
\[ L = \frac{\left( 3^{4} \cdot 3^{-2} \right)^{2}}{3^{2} \cdot 3^{-3}} \]
2º Passo: aplicar as propriedades de potências.
Multiplicação no numerador:
\[ 3^{4} \cdot 3^{-2} = 3^{4 - 2} = 3^{2} \Rightarrow \left( 3^{2} \right)^{2} = 3^{4} \]
No denominador:
\[ 3^{2} \cdot 3^{-3} = 3^{2-3} = 3^{-1} \]
Agora temos:
\[ L = \frac{3^{4}}{3^{-1}} = 3^{4-(-1)} = 3^{4+1} = 3^{5} \]
✅ Gabarito: Letra A
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 10
Considere a inequação
\[
x^{2} - 8x + 16 \geq 0
\]
Dadas as afirmativas,
I. A inequação é satisfeita para todo valor de \(x\).
II. Existe um único valor de \(𝑥\) que torna \(x^{2} - 8x + 16 = 0\).
III. Existem valores de \(𝑥\) que tornam \(x^{2} - 8x + 16\) negativo.
verifica-se que está/ão correta/s:
🎓 Dica do Professor:
Note que o polinômio pode ser fatorado como um trinômio quadrado perfeito:
\[
a^2 - 2ab + b^2 = (a - b)^2
\]
Depois de fatorar, avalie o sinal da expressão usando o fato de que quadrados são sempre maiores ou iguais a zero.
✍️ Comentário do professor:
Temos a inequaçãa:\[ x^2 - 8x + 16 \geq 0 \]
1º Passo: Fatoração do trinômio.
Vamos tentar reescrevê-lo como um quadrado perfeito.
\[ x^2 - 8x + 16 = (x - 4)^2 \]
2º Passo: Reescrever a inequação.
A inequação se torna:
\[ (x - 4)^2 \geq 0 \]
Essa expressão é o quadrado de um número real, logo nunca é negativo. Ou seja:
\[ (x−4)^2 \geq 0 \text{ é verdadeira para todo valor de } x. \]
3º Passo: Análise das afirmativas.
I. A inequação é satisfeita para todo valor de x.
✅ Verdadeiro! \[ \text{Pois} \,\, (x - 4)^2 \geq 0 \,\, \text{é sempre verdadeira.} \]
II. Existe um único valor de x que torna \(x^2 - 8x + 16 = 0\).
✅ Verdadeiro!
\[ x^2 - 8x + 16 = 0 \] \[ (x - 4)^2 = 0 \] \[ x-4 = 0 \Rightarrow x=4 \]
III. Existem valores de x que tornam \(x^2 - 8x + 16\) negativo.
\(\color{Red} Falso\).
\(\text{Como já vimos,} \,\, (x - 4)^2 \geq 0, \,\, \text{então nunca é negativo.}\)
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 11
Ao começar um curso de origami (dobradura em papel), Maria inicia alguns exercícios de dobraduras para aprimorar sua técnica. Após algum treino, ela se depera com um exercício de transformar figuras planas em triângulos, usando apenas as dobraduras, sem que seja permitido o recorte do papel. No exercício em questão, Maria inicia com um polígono regular de 8 (oito) lados. Diante disso, o número mínimo de dobraduras que Maria precisa fazer para que o polígono seja dobrado em um triângulo é:
🎓 Dica do Professor:
Pense que a cada dobradura, Maria pode reduzir o número de lados do polígono de maneira controlada. A ideia é pensar em quantas dobraduras são necessárias para transformar um polígono de 8 lados em um triângulo (3 lados).
Reflita sobre como o número de lados diminui após cada dobra.
✍️ Comentário do professor:
Maria começa com um polígono regular de 8 lados — ou seja, um octógono regular.Ela precisa dobrar esse polígono até que ele se transforme em um triângulo, que tem 3 lados.
💡 Como não é permitido cortar o papel, cada dobradura precisa reduzir o número de lados visíveis da figura. Vamos imaginar que, a cada dobra bem feita, Maria pode esconder 1 lado (ou uma parte da borda do polígono), de modo que ao final sobrem 3 lados visíveis.
O objetivo é transformar 8 lados em 3. Para isso, Maria precisa eliminar \(8 - 3 = 5\) lados.
👉 Logo, no mínimo, são necessárias 5 dobraduras, uma para esconder cada lado extra.
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 12
Considere a expressão
\[
\left( x + 4\right)^2 + \left( x - 3\right) \cdot \left( x + 3\right) - \left( 2x - 1 \right)^{2}
\]
A forma simplificada dessa expressão é:
🎓 Dica do Professor:
Revise os seguintes produtos notáveis antes de resolver:
1. Quadrado da soma:
\[
(a + b)^{2} = a^{2} + 2ab + b^{2}
\]
2. Quadrado da diferença:
\[
(a - b)^{2} = a^{2} - 2ab + b^{2}
\]
3. Produto da soma pela diferença:
\[
(a + b)(a - b) = a^{2} - b^{2}
\]
Aplique essas fórmulas a cada parte da expressão.
✍️ Comentário do professor:
Vamos desenvolver cada parte separadamente:1) Desenvolvendo \((x + 4)^2\):
\[ (x+4)^{2} = x^{2} + 2x \cdot 4 + 4^{2} = x^{2} + 8x + 16 \]
2) Desenvolvendo \((x - 3) \cdot (x+3)\):
É um produto da soma pela diferença:
\[ (x-3)(x+3) = x^{2} - 9 \]
3) Desenvolvendo \((2x - 1)^{2}\):
\[ (2x - 1)^{2} = (2x)^{2} - 2 \cdot 2x \cdot 1 + 1^{2} = 4x^{2} - 4x + 1 \]
Agora juntamos tudo na expressão completa:
\[ \left( x + 4\right)^2 + \left( x - 3\right) \cdot \left( x + 3\right) - \left( 2x - 1 \right)^{2} \]
Substituindo:
\[ \left( x^{2} + 8x + 16 \right) + \left( x^{2} - 9 \right) - \left( 4x^{2} - 4x + 1 \right) \]
Removendo os parênteses e reorganizando os termos:
\[ x^2 + 8x + 16 + x^2 - 9 - 4x^2 + 4x - 1 \]
Organizando:
\[ x^2 + x^2 - 4x^2 + 8x + 4x + 16 - 9 - 1 = -2x^2 + 12x + 6 \]
\[ \boxed{2 \cdot (-x^2 + 6x + 3)} \]
Gabarito: Letra E
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 13
Ao longo dos últimos anos, a obesidade infantil tem se tornado um problema cada vez mais preocupante no Brasil e no mundo. Segundo dados do Ministério da Saúde, em conjunto com as diretrizes da Sociedade Brasileira de Pediatria (SBP) e da Organização Mundial da Saúde (OMS), a quantidade de calorias recomendada para crianças entre 9 (nove) anos e 12 anos varia entre 1.800 e 2.200 calorias por dia, dependendo do nível de atividade física. No caso de Maria, em seu café da manhã, ela consumiu 300 g de macaxeira cozida e 250 g de cuscuz. Além disso, no almoço e ao longo do dia, Maria ingeriu mais 1.200 calorias.
Sabendo-se que 100 g de macaxeira cozida contém 125 calorias e que 100 g de cuscuz contém 112 calorias, assinale a alternativa correta que representa a porcentagem de calorias que Maria já consumiu, considerando-se a recomendação diária de 2.000 calorias.
🎓 Dica do Professor:
Use a regra de três para calcular quantas calorias ela ingeriu de macaxeira e de cuscuz, depois some com as 1.200 calorias informadas. Por fim, calcule a porcentagem em relação ao total recomendado (2.000 calorias):
\[
\text{Porcentagem} = \left( \frac{\text{Total consumido}}{2000} \right) \cdot 100
\]
✍️ Comentário do professor:
🍠 1) Calorias da macaxeira (300 g):Sabemos que 100 g → 125 cal
Então:
\[ \text{300 g} = 3 \cdot 125 = \text{375 calorias} \]
🌽 2) Calorias do cuscuz (250 g):
\[ \text{100 g} \to \text{112 cal} \] \[ \text{50 g} \to \text{56 cal} \]
Considere que:
\[ \text{250 g} = \text{100 g} + \text{100 g} + \text{50 g} \]
Logo,
\[ \text{250 g} \to \text{112 cal} + \text{112 cal} + \text{56 cal} = \text{280 calorias} \]
➕ 3) Total consumido no café da manhã:
\[ \text{375 calorias} + \text{280 calorias} = \text{655 calorias} \]
🍽️ 4) Total ingerido no dia:
\[ \text{655 calorias} + \text{1.200 calorias} = \text{1.855 calorias} \]
📊 5) Cálculo da porcentagem:
\[ \frac{1.855}{2000} \cdot 100 = 92,75\% \]
✅ Gabarito: Letra A
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 14
Ana estuda em uma escola na qual a média final de Matemática é calculada a partir das notas das quatro provas realiza longo dos bimestres do ano. A média final é dada pela fórmula:
\[
MF = \frac{B_{1} + B_{2} + B_{3} + B_{4}}{4}
\]
em que, \(B_{1}\), \(B_{2}\), \(B_{3}\) e \(B_{4}\) são as notas de cada bimestre. Para ser aprovada, Ana precisa obter uma média final de, pelo menos, 6,0. Sabe-se que Ana tem as notas de 3 (três) bimestres: \(B_{1} = 5,5\), \(B_{2} = 6,0\) e \(B_{3} = 7,0\).
Assinale a alternativa correta que apresenta a nota mínima \(B_{4}\) de para que Ana seja aprovada.
🎓 Dica do Professor:
Para calcular a média final, soma-se todas as notas e divide-se por 4.
Você já sabe 3 das notas. Monte uma equação com a incógnita \(B_{4}\) e descubra qual é o menor valor possível para que a média seja, no mínimo, 6,0.
✍️ Comentário do professor:
Temos a fórmula da média final:\[ MF = \frac{B_{1} + B_{2} + B_{3} + B_{4}}{4} \]
Sabemos que:
• \(B_{1} = 5,5\)
• \(B_{2} = 6,0\)
• \(B_{3} = 7,0\)
• \(B_{4} = ?\)
Considere que para ter a nota mínima teremos a média mínima que nesse caso é 6,0.
\[ \frac{5,5 + 6,0 + 7,0 + B_{4}}{4} = 6,0 \]
Some os valores conhecidos:
\[ \frac{18,5 + B_{4}}{4} = 6,0 \] \[ 18,5 + B_{4} = 4 \cdot 6,0 \] \[ 18,5 + B_{4} = 24 \Rightarrow B_{4} = 24 - 18,5 \Rightarrow B_{4} = 5,5 \]
Assim, podemos concluir que, para tirar a menor média, é preciso que a nota \(B_{4} = 5,5\).
✅ Resposta correta: Letra C) \( B_4 \geq 5,5 \)
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 15
Ao realizar a prova de seleção do IFAL, um estudante, antes de entrar para a prova, comprou duas canetas reservas, duas garrafas de água e uma barra de chocolate, efetuando o pagamento com uma nota de R$ 50,00. Se cada água custou R$ 2,70, cada caneta R$ 0,80 e a barra de chocolate R$ 11,00, o troco que o estudante recebeu foi
🎓 Dica do Professor:
Some o valor de cada item multiplicado pela quantidade.
Depois, subtraia o valor total da compra do dinheiro dado (R$ 50,00).
Isso te dará o troco.
✍️ Comentário do professor:
1️⃣ Valor das canetas:\[ 2 \times 0,80 = 1,60 \]
2️⃣ Valor das águas:
\[ 2 \times 2,70 = 5,40 \]
3️⃣ Valor do chocolate:
\[ 11,00 \]
4️⃣ Soma do total gasto:
\[ 1,60 + 5,40 + 11,00 = 18,00 \]
5️⃣ Troco:
\[ 50,00 - 18,00 = 32,00 \]
✅ Resposta correta: Letra C) R$ 32,00
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 16
Uma equipe de estudantes do IFAL está desenvolvendo um modelo de inteligência artificial para prever o consumo de energia em um laboratório. O consumo total é estimado por um modelo polinomial que considera o número de dispositivos ligados, 𝑥, e o tempo de uso em horas, 𝑦. O polinômio que modela o consumo de energia, medido em kWh, é dado por:
\[
P(x,y) = 2x^{2} + 3xy - 4y^{2} + 5
\]
Para efetuar um teste no modelo de consumo e verificar sua precisão, os estudantes deixam 3 (três) dispositivos ligados por 2 (duas) horas. Assinale a alternativa correta que apresenta o consumo total estimado pelo modelo.
🎓 Dica do Professor:
Substitua os valores de x e y na expressão do polinômio. Faça cada operação com calma, respeitando a ordem das operações: potência, depois multiplicações, depois, adições/subtrações.
✍️ Comentário do professor:
• \(x = 3\) número de dispositivos ligados• \(y = 2\) tempo de uso em horas
Substituindo na fórmula: \[ P(3,2) = 2 \cdot (3)^{2} + 3 \cdot 3 \cdot 2 - 4 \cdot (2)^{2} + 5 \] \[ P(3,2) = 2 \cdot 9 + 18 - 16 + 5 \] \[ P(3,2) = 18 + 18 - 16 + 5 \] \[ P(3,2) = 25 \]
✅ Resposta correta: Letra D) 25 kWh
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 17
Luísa está organizando a sua festa de aniversário e decidiu encomendar balões e chapéus de festa. Cada balão custa R$ 3,00 e cada chapéu custa R$ 5,00. Ela gastou ao todo R$ 90,00 e comprou 22 itens entre balões e chapéus. Quantos balões e chapéus Luísa comprou?
🎓 Dica do Professor:
Use um sistema de equações:
• Uma equação para o número total de itens
• Outra equação para o valor total gasto
Chame:
• x = número de balões
• y = número de chapéus
Você sabe:
• Cada balão custa R$ 3,00
• Cada chapéu custa R$ 5,00
• Luísa comprou 22 itens no total
• E gastou R$ 90,00
✍️ Comentário do professor:
1️⃣ Monte o sistema:1. Total de itens:
\[ x + y = 22 \quad \text{(1)} \]
2. Total de gastos
\[ 3x + 5y = 90 \quad \text{(2)} \]
2️⃣ Isolando uma variável na equação (1):
\[ y = 22 - x \quad \text{(3)} \]
3️⃣ Substituindo na equação (2):
\[ 3x + 5(22 - x) = 90 \] \[ 3x + 110 - 5x = 90 \] \[ -2x + 110 = 90 \] \[ -2x = 90 - 110 = -20 \] \[ x = 10 \]
4️⃣ Agora, calcule y:
\[ y = 22 - x = 22 - 10 = 12 \]
✅ Resposta correta: Letra C) 10 balões e 12 chapéus
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"
Questão 18
Durante um atendimento de emergência, um paciente recebe uma infusão intravenosa de soro fisiológico a uma taxa de 125 mL por hora. Sabendo-se que o paciente precisa receber 1,25 litros de soro, assinale a alternativa correta que contém o tempo necessário para completar a infusão.
🎓 Dica do Professor:
Converta os litros para mililitros (porque a taxa está em mL/h) e depois divida o volume total pela taxa de infusão.
✍️ Comentário do professor:
1️⃣ Converta litros para mililitros:\[ 1,25 \text{ litros} = 1,25 \times 1000 = \text{1250 mL} \]
2️⃣ A taxa de infusão é de:
\[ \text{125 mL por hora} \]
3️⃣ Divida o total de soro pela taxa de infusão:
\[ \frac{1250}{125} = 10 \]
✅ Resposta correta: Letra C) 10 horas
Vídeo gabarito:
"O vídeo gabarito ainda não está disponível"

✍️ Comentário do professor:
Resolução passo a passo
A expressão é: \[ N = \sqrt{50} + 3 \cdot \sqrt{8} - 2 \cdot \sqrt{18} \] Vamos simplificar cada raiz:
1º você deve simplificar: \(\sqrt{50}\)
\[ \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt {2} = 5 \cdot \sqrt{2} \]
2º você deve simplificar: \(\sqrt{8}\)
\[ \sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt {2} = 2 \cdot \sqrt{2} \]
3º você deve simplificar: \(\sqrt{18}\) \[ \sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt {2} = 3 \cdot \sqrt{2} \] Agora vamos substituir cada simplificação e realizar as operações: \[ N = \sqrt{50} + 3 \cdot \sqrt{8} - 2 \cdot \sqrt{18} \] \[ N = 5 \cdot \sqrt{2} + 3 \cdot 2 \cdot \sqrt{2} - 2 \cdot 3 \cdot \sqrt{2} \] \[ N = 5 \cdot \sqrt{2} + 6 \cdot \sqrt{2} - 6 \cdot \sqrt{2} \] \[ N = (5 + 6 - 6) \cdot \sqrt{2} \] \[ N = 5 \cdot \sqrt{2} \]