E aí, pessoal! Tudo bem com vocês? No artigo anterior, vimos que a função afim, é uma função \(f:\mathbb{R\rightarrow \mathbb{R}}\) definida pela seguinte lei de formação:
onde a e b são coeficientes determinados por números reais diferentes de zero.
Nesse artigo, vamos dar um passo além e desvendar o fascinante mundo do gráfico da função afim! Preparem-se para uma aventura visual que vai tornar a função afim uma ferramenta matemática ainda mais interessante!
Conteúdos
O Gráfico da Função Afim: Uma Reta com Personalidade
O gráfico da função afim, como já foi visto no 9o ano, é sempre uma reta e, se você quer saber o porquê fala nos comentários que vou postar um arquivo te mostrando isso passa a passo. Vou esperar seu comentário!!! Mas como essa reta se comporta? É isso que vamos descobrir!
Coeficientes da Função Afim: Os Arquitetos da Reta
Antes de partirmos para o gráfico, precisamos conhecer melhor os “personagens” que constroem a função afim. Lembram daqueles coeficientes que aparecem na lei de formação \(f(x)= a\cdot x+b\)? Pois é, eles têm nomes e papéis super importantes!
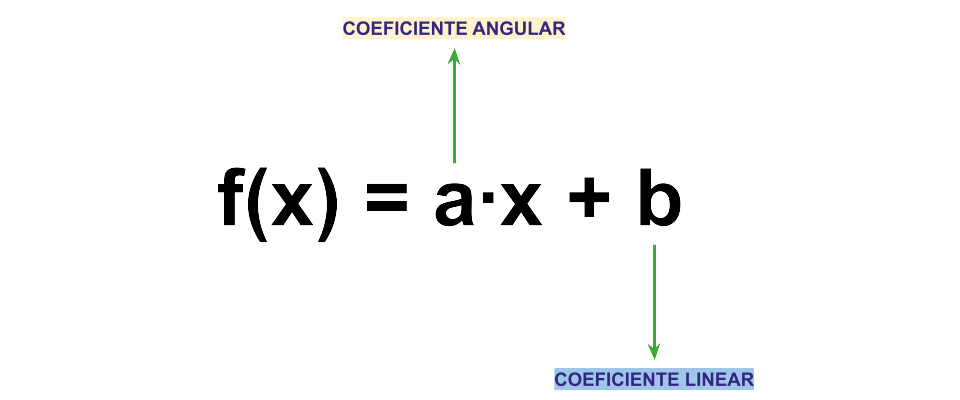
Agora que sabemos o nome de cada um dos coeficientes vamos dar um passo além! Vamos conectar tudo isso ao gráfico da função afim. E o melhor: de um jeito leve e descontraído, sem perder a essência matemática. Então, pegue seu lápis, baixa o nosso ebook e vamos nessa!
A Inclinação da Reta e o Coeficiente Angular

O coeficiente angular (a) é o grande responsável pela inclinação da reta. Ele nos diz o quanto a reta “sobe” ou “desce” conforme nos movemos para a direita no eixo x.
- Se a > 0, a reta é crescente. Isso significa que, à medida que x aumenta, y também aumenta. Imagine uma subida suave!
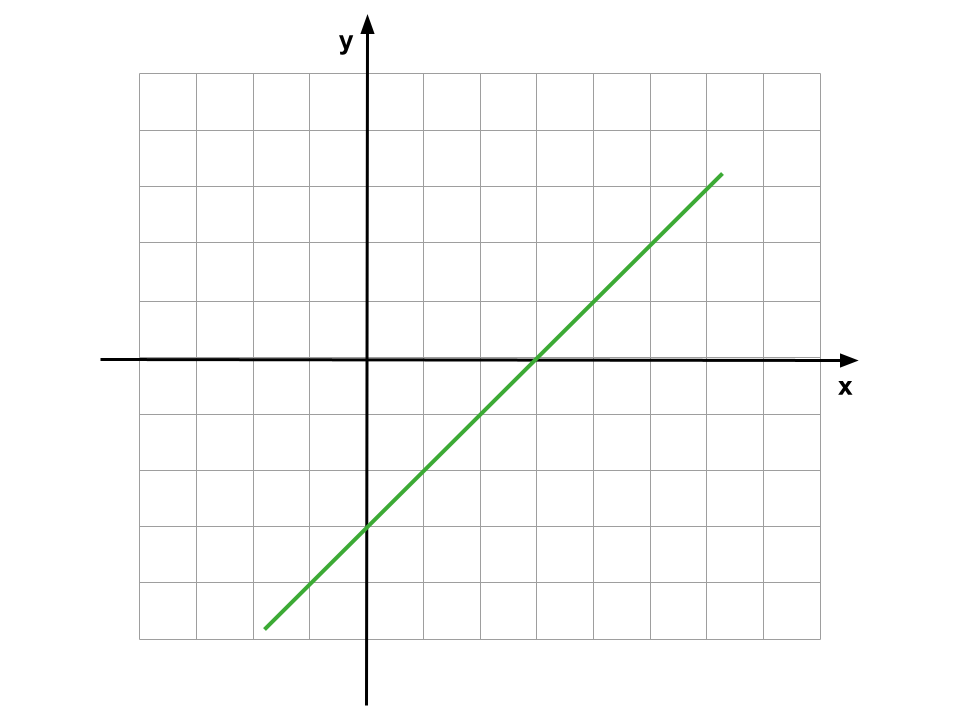
- Se a < 0, a reta é decrescente. Aqui, à medida que x aumenta, y diminui. É como uma descida.
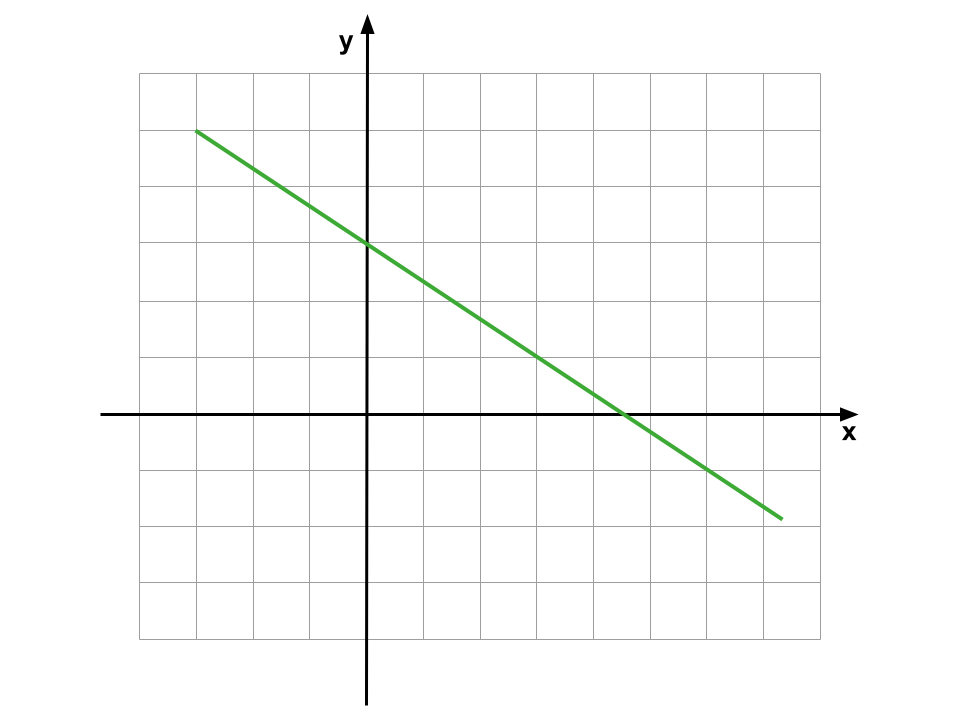
O Coeficiente Linear e a Interseção com o Eixo y

O coeficiente linear (b) é o termo independente de x e indicará o ponto onde a reta corta o eixo y. Ele nos dá uma “âncora” para começar a desenhar a reta.
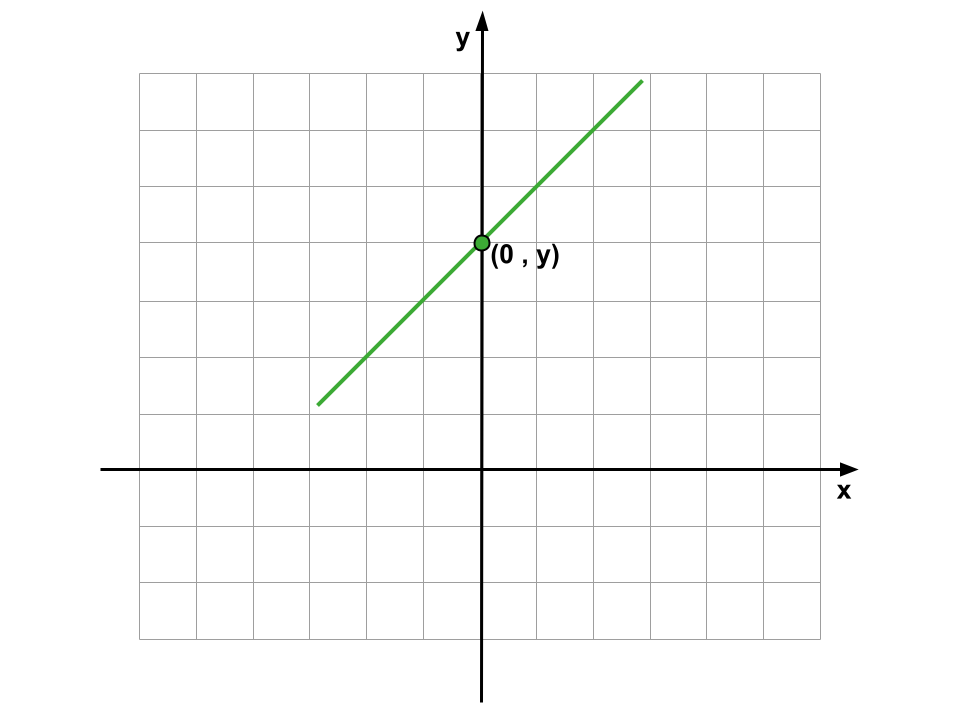
Veja que, quando da reta intercepta o eixo 𝑦, 𝑥 = 0. Então, para calcular o valor do Coeficiente Linear, basta igualar 𝒙 a zero.
$$ y = a\cdot 0 + b$$
$$ y = b$$
Considerando uma função afim definida por \(f(x)= a\cdot x+b\), com a e b não nulos.
| ESQUEMATIZANDO | |
| a > 0 | a < 0 |
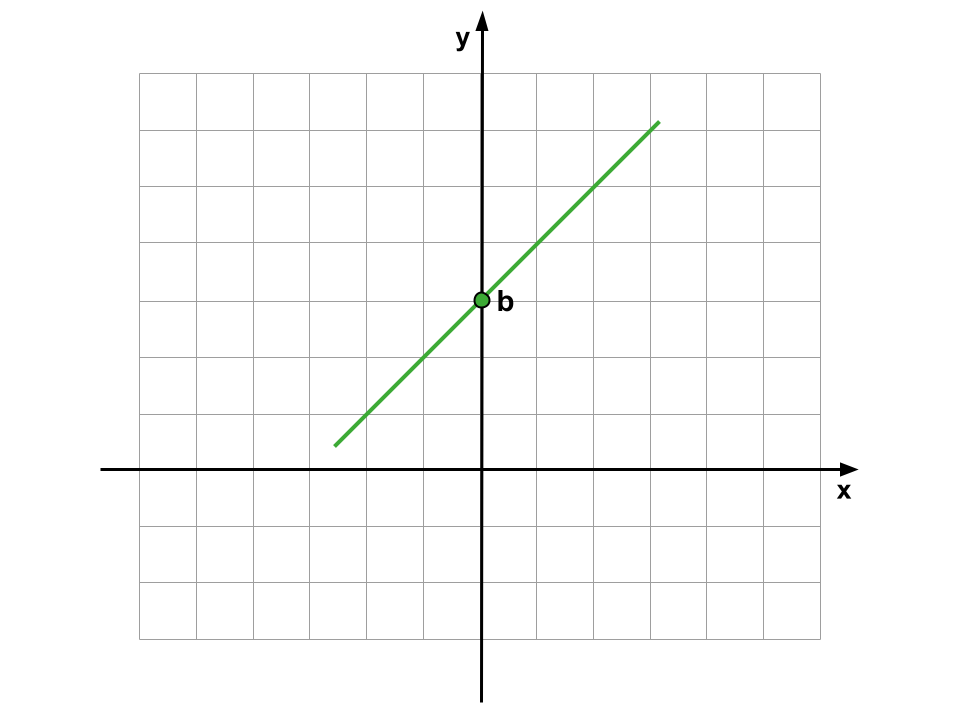 | 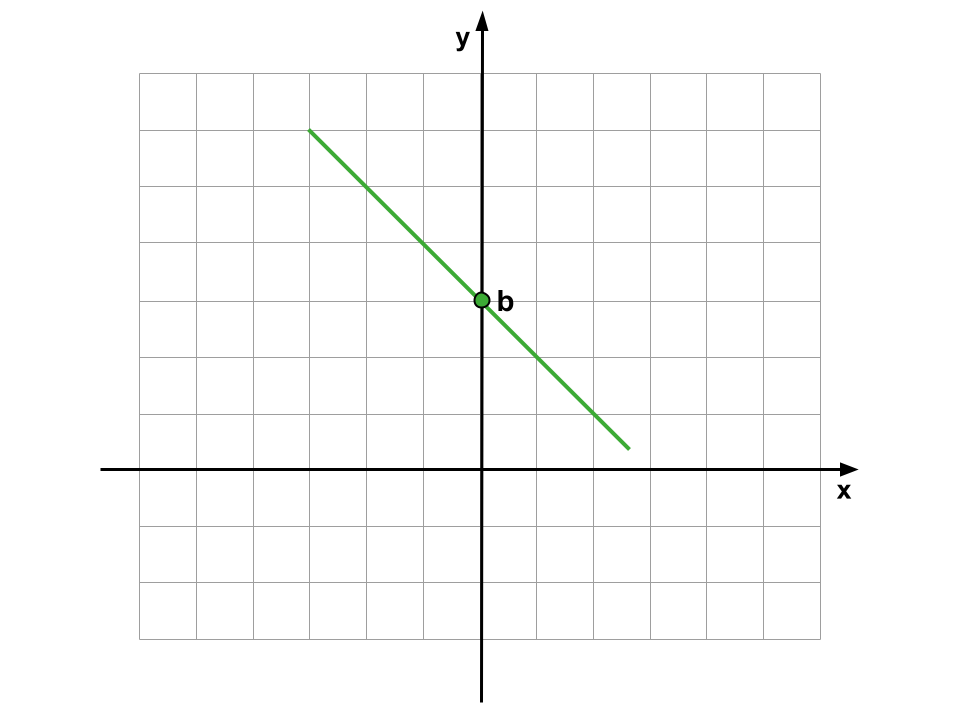 |
Vamos resolver os exercícios abaixo para fixar bem o conteúdo sobre Coeficientes. Conteúdo esse, que “despenca em provas”.
Exercícios de matemática resolvidos – Função Afim – Agora é Com Você
Questão 01
(ProfMicael-2025) A função afim, também conhecida como função polinomial do 1º grau, e é definida pela lei de formação \(f(x)=a\cdot x +b\). Uma função afim é crescente quando:
A) a > 0
B) a < 0
C) a = 0
D) b > 0
E) b < 0
Questão 02
(ProfMicael-2025) Dentre as funções abaixo, pode-se dizer que a única que uma função afim DECRESCENTE é:
A) \(f(x)=2\)
B) \(f(x)=3\cdot x\)
C) \(f(x)=4-5\cdot x\)
D) \(f(x)=-4\cdot x\)
E) \(f(x)=2\cdot x -6\)
Questão 03
(ProfMicael-2025) Na figura abaixo temos o gráfico de uma função afim definida por uma lei de formação do tipo \(f(x)=a\cdot x + b\), onde \(a,b\in \mathbb{R}\).
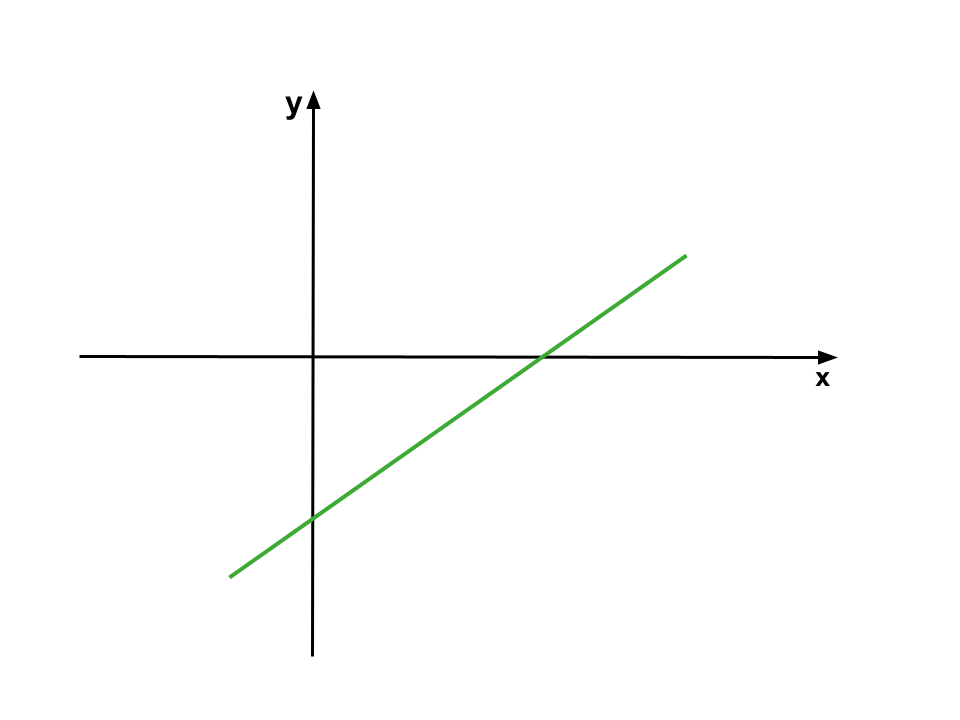
Analisando esse gráfico e a sua relação com os coeficientes 𝑎 e 𝑏, qual das alternativas traz uma função afim que possa representa tal gráfico?
A) \( f(x) = 2x + 3\)
B) \( f(x) = -4x + 1\)
C) \( f(x) = 3x – 1\)
D) \( f(x) = -2x – 3\)
E) nenhuma das alternativas acima
Questão 04
(ProfMicael-2025) A figura abaixo representa as funções \(f(x)=a\cdot x + b\) e \(g(x)=c\cdot x + d\) que foram desenhadas no mesmo plano cartesiano.
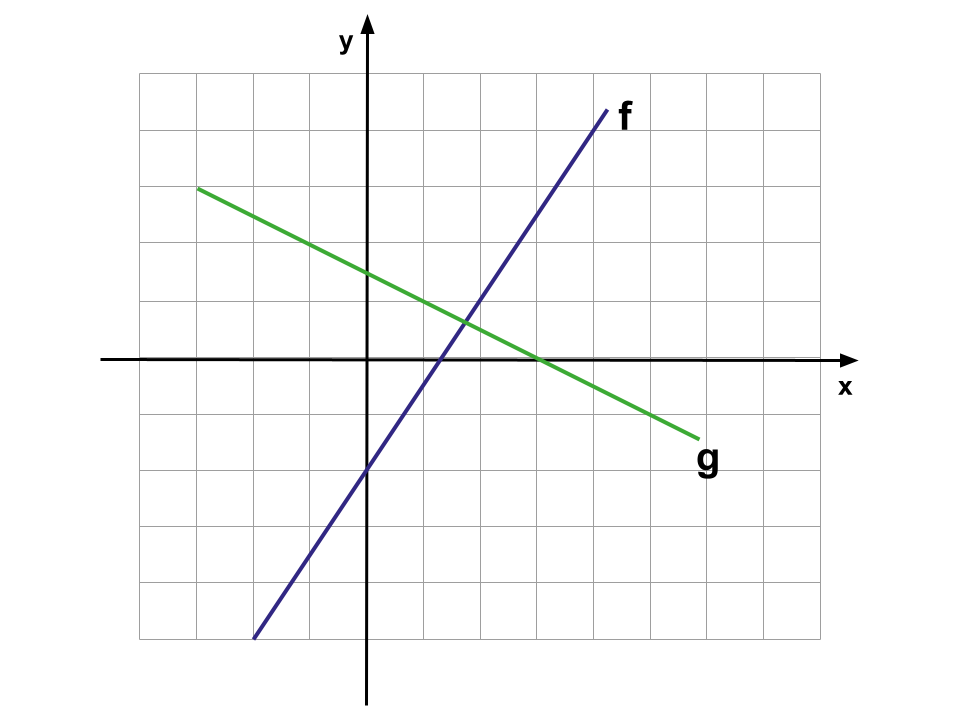
Sobre os coeficientes a, b, c e d, podemos afirmar que:
A) a > 0 | b > 0 | c < 0 | d < 0
B) a < 0 | b < 0 | c > 0 | d > 0
C) a > 0 | b < 0 | c < 0 | d > 0
D) a > 0 | b > 0 | c > 0 | d > 0
E) a < 0 | b < 0 | c < 0 | d < 0
Questão 05
(ProfMicael-2025) Qual das alternativas abaixo apresenta um gráfico que pode representar a função \(f(x)=2\cdot x – 4\)?
| A) | B) |
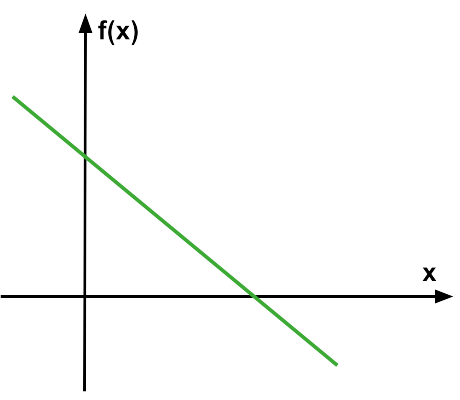 | 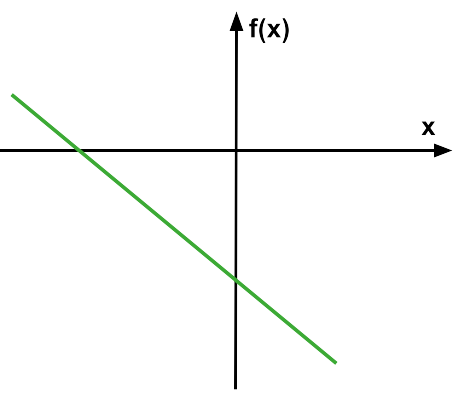 |
| C) | D) |
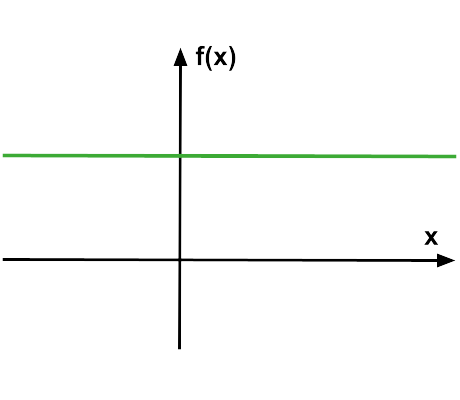 | 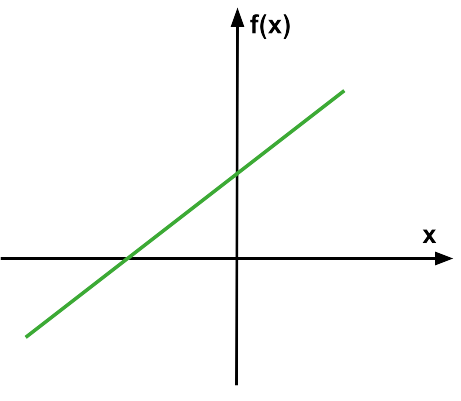 |
| E) | |
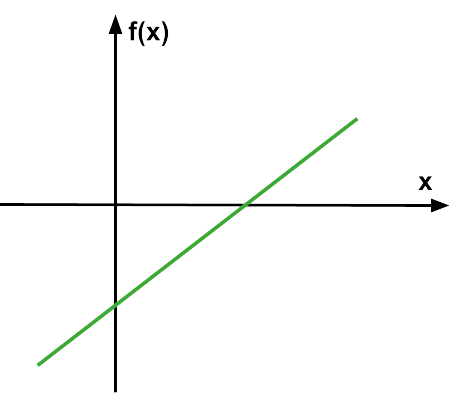 |
A Raiz da Função e a Interseção com o Eixo x
No Lembram da raiz da função afim? Aquela que a gente calcula igualando a função a zero? Pois é, ela tem uma relação direta com o gráfico! A raiz da função é o ponto onde a reta corta o eixo x.
O zero da função (ou raiz) é o valor de x que faz com que y seja zero. No gráfico, esse ponto é super importante porque é onde a reta “toca” o eixo x. Ele nos dá uma referência para entender o comportamento da função.

Resumindo: Como Tudo se Conecta?
Agora que já conhecemos os coeficientes e seus papéis, vamos juntar tudo:
- O coeficiente angular (a) define a inclinação da reta e se ela é crescente ou decrescente.
- O coeficiente linear (b) nos diz onde a reta corta o eixo y.
- A raiz da função nos mostra onde a reta corta o eixo x.
Juntos, esses elementos nos permitem desenhar e interpretar o gráfico da função afim com precisão.
E Agora, Praticar!
Que tal pegar algumas funções afins e tentar desenhar seus gráficos? Escolha valores para a e b, calcule a raiz, identifique se a função é crescente ou decrescente e veja como tudo se encaixa. A matemática fica muito mais interessante quando a gente consegue visualizá-la, não é mesmo? Pensando nisso tenho [um artigo] para que você possa colocar tudo isso em prática, Vai lá!!!
E aí, gostaram de descobrir os segredos do gráfico da função afim? No próximo artigo, vamos explorar mais aplicações práticas dessa função. Até lá, continuem praticando e se divertindo com a matemática! 😊
Quero muito saber o que você achou desse artigo. Comenta ai!!!




